题目内容
14. 如图,已知AD平分∠BAC,AB=AC,CE∥BF,则此图中全等三角形有( )
如图,已知AD平分∠BAC,AB=AC,CE∥BF,则此图中全等三角形有( )| A. | 2对 | B. | 3 对 | C. | 4对 | D. | 5对 |
分析 利用等腰三角形的性质得出BD=CD,再利用全等三角形的判定方法得出即可.
解答  解:∵AD平分∠BAC,AB=AC,
解:∵AD平分∠BAC,AB=AC,
∴BD=CD,
在△ABD和△ACD中$\left\{\begin{array}{l}{AB=AC}\\{AD=AD}\\{BD=CD}\end{array}\right.$,
∴△ABD≌△ACD(SSS),
∵CE∥BF,
∴∠ECB=∠FBC,
在△EDC和△FDB中
$\left\{\begin{array}{l}{∠ECD=∠FBD}\\{DC=BD}\\{∠CDE=∠BDF}\end{array}\right.$,
∴△EDC≌△FDB(ASA),
故此图中全等三角形有2对.
故选:A.
点评 此题主要考查了全等三角形的判定以及等腰三角形的性质,正确应用全等三角形的判定方法是解题关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
3.
| 多项式 | 2x3y-4x2y2-3x5 | 2x-1 | 2x2-x-3 | x2-2x-4x3-1 |
| 项 | 2x3y,-4x2y2,-3x5 | 2x,-1 | 2x2,-x,-3 | x2,-2x,-4x3,-1 |
| 最高次项 | -3x5 | 2x | 2x2 | -4x3 |
| 常数项 | 0 | -1 | -3 | -1 |
| 几次几项式 | 五次三项式 | 一次二项式 | 二次三项式 | 三次四项式 |
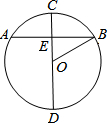 如图,⊙O的直径CD垂直弦AB于点E,且CE=2,AB=8,则DE的长为8.
如图,⊙O的直径CD垂直弦AB于点E,且CE=2,AB=8,则DE的长为8.
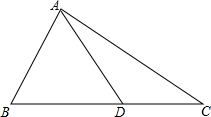 已知在△ABC中,∠B=60°,AD=14,CD=12,S△ADC=30$\sqrt{3}$,求BD的长.
已知在△ABC中,∠B=60°,AD=14,CD=12,S△ADC=30$\sqrt{3}$,求BD的长.