题目内容
4.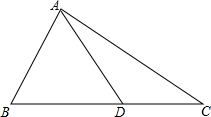 已知在△ABC中,∠B=60°,AD=14,CD=12,S△ADC=30$\sqrt{3}$,求BD的长.
已知在△ABC中,∠B=60°,AD=14,CD=12,S△ADC=30$\sqrt{3}$,求BD的长.
分析 作AE⊥BD于E,则∠AEB=∠AED=90°,由三角形的面积求出AE=5$\sqrt{3}$,由勾股定理求出DE=$\sqrt{A{D}^{2}-A{E}^{2}}$=11,再由三角函数求出BE,即可得出BD的长.
解答 解:作AE⊥BD于E,如图所示: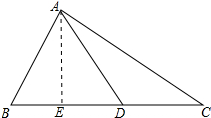
则∠AEB=∠AED=90°,
∵S△ADC=$\frac{1}{2}$CD×AE=30$\sqrt{3}$,
∴$\frac{1}{2}$×12×AE=30$\sqrt{3}$,
∴AE=5$\sqrt{3}$,
∴DE=$\sqrt{A{D}^{2}-A{E}^{2}}$=$\sqrt{1{4}^{2}-(5\sqrt{3})^{2}}$=11,
∵∠B=60°,
∴BE=$\frac{\sqrt{3}}{3}$AE=$\frac{\sqrt{3}}{3}$×5$\sqrt{3}$=5,
∴BD=BE+DE=5+11=16.
点评 本题考查了勾股定理、三角函数、三角形面积的计算方法;熟练掌握勾股定理,通过作辅助线构造直角三角形是解决问题的关键.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
14. 如图,已知AD平分∠BAC,AB=AC,CE∥BF,则此图中全等三角形有( )
如图,已知AD平分∠BAC,AB=AC,CE∥BF,则此图中全等三角形有( )
 如图,已知AD平分∠BAC,AB=AC,CE∥BF,则此图中全等三角形有( )
如图,已知AD平分∠BAC,AB=AC,CE∥BF,则此图中全等三角形有( )| A. | 2对 | B. | 3 对 | C. | 4对 | D. | 5对 |
12.-m+3n-5的相反数与m+3n的差为( )
| A. | 6n-5 | B. | 6n+5 | C. | 2m+5 | D. | -6n+5 |
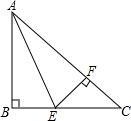 如图,在Rt△ABC中,∠ABC=90°,AE是角平分线,若BE:EC=3:5,BC=4cm,则点E到AC的距离为$\frac{3}{2}$cm.
如图,在Rt△ABC中,∠ABC=90°,AE是角平分线,若BE:EC=3:5,BC=4cm,则点E到AC的距离为$\frac{3}{2}$cm. 如图,∠C=90°,∠1=∠2,若BC=20,BD=15,则点D到AB的距离为5.
如图,∠C=90°,∠1=∠2,若BC=20,BD=15,则点D到AB的距离为5.