题目内容
9.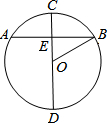 如图,⊙O的直径CD垂直弦AB于点E,且CE=2,AB=8,则DE的长为8.
如图,⊙O的直径CD垂直弦AB于点E,且CE=2,AB=8,则DE的长为8.
分析 先根据垂径定理求出BE的长,再设OB=r,则OE=r=2,再根据勾股定理求出r的值,进而得出OE的值,由此可得出结论.
解答 解:∵⊙O的直径CD垂直弦AB于点E,AB=8,
∴BE=$\frac{1}{2}$AB=4.
设OB=r,则OE=r=2,
在Rt△OBE中,
∵OE2+BE2=OB2,即(r-2)2+42=r2,解得r=5,
∴OE=5-2=3,
∴DE=OE+OD=3+5=8.
故答案为:8.
点评 本题考查的是垂径定理,熟知平分弦的直径平分这条弦,并且平分弦所对的两条弧是解答此题的关键.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
17.在函数$y=\frac{{\sqrt{x+1}}}{2x-1}$中,自变量x的取值范围是( )
| A. | x≥-1 | B. | x>-1且x≠$\frac{1}{2}$ | C. | x≥-1且x≠$\frac{1}{2}$ | D. | x≥-1 |
14. 如图,已知AD平分∠BAC,AB=AC,CE∥BF,则此图中全等三角形有( )
如图,已知AD平分∠BAC,AB=AC,CE∥BF,则此图中全等三角形有( )
 如图,已知AD平分∠BAC,AB=AC,CE∥BF,则此图中全等三角形有( )
如图,已知AD平分∠BAC,AB=AC,CE∥BF,则此图中全等三角形有( )| A. | 2对 | B. | 3 对 | C. | 4对 | D. | 5对 |
1.以边长为1的正方形ABCD的顶点A为圆心,以$\sqrt{2}$为半径作⊙A,则点C关于⊙A的位置关系是( )
| A. | 点C 在⊙A内 | B. | 点C在⊙A上 | C. | 点C在⊙A外 | D. | 不能确定 |
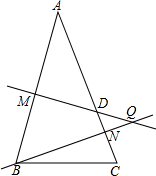 如图,在△ABC中,△ABC中,∠ABC=∠C,AB的垂直平分线MQ交AC于D,CD的垂直平分线恰好过点B,求∠A的度数.
如图,在△ABC中,△ABC中,∠ABC=∠C,AB的垂直平分线MQ交AC于D,CD的垂直平分线恰好过点B,求∠A的度数.