题目内容
19．在平面直角坐标系中，点P（2，0），Q（2，4），在y轴有一点M，若PM+QM最小，则M的坐标为（0，2）．分析 作出点P关于y轴的对称点N，连接NQ交y轴于点M．由轴对称的性质可知MP+QM=MN+MQ=，由两点之间线段最短可知：当M、Q、N在一条直线上时，MP+MQ有最小值，利用勾股定理求得答案即可．
解答 解：如图所示：作出点P关于y轴的对称点N，连接NQ交y轴于点M．．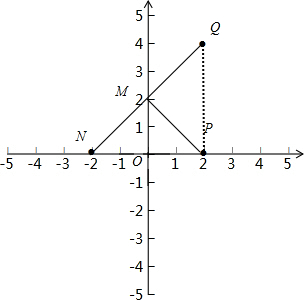
由轴对称的性质可知：MP=MN，
∴MP+MQ=MN+MQ，
由两点之间线段最短可知：当M、Q、N在一条直线上时，MP+MQ有最小值．
设直线QN所在直线的解析式为y=kx+b，
将点Q（2，4）、N（-2，0）代入得：
$\left\{\begin{array}{l}{2k+b=4}\\{-2k+b=0}\end{array}\right.$，
解得：k=1，b=2．
∴直线QN的解析式为y=x+2．
将x=0代入得y=2，
∴点M的坐标为（0，2）
故答案为：（0，2）．
点评 本题主要考查的是轴对称-路径最短问题、待定系数法求函数的解析式、一次函数与y轴的交点，明确M、Q、N在一条直线上时，MP+MQ有最小值是解题的关键．
练习册系列答案
天天向上口算本系列答案
相关题目
9．下列说法中正确的是（ ）
| A． | 两个全等三角形成轴对称 | |
| B． | 两个三角形关于某直线对称，不一定全等 | |
| C． | 线段AB的对称轴垂直平分AB | |
| D． | 直线MN垂直平分线段AB，则直线MN是线段AB的对称轴 |
如图，已知边长为6的等边三角形ABC纸片，点E在AC边上，点F在AB边上，沿EF折叠，使点A落在BC边上的点D的位置，且ED⊥BC，则CE的长是24-12$\sqrt{3}$．
14．
如图，已知AD平分∠BAC，AB=AC，CE∥BF，则此图中全等三角形有（ ）
如图，已知AD平分∠BAC，AB=AC，CE∥BF，则此图中全等三角形有（ ）| A． | 2对 | B． | 3 对 | C． | 4对 | D． | 5对 |
4．
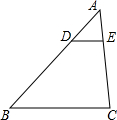如图，在△ABC中，DE∥BC，$\frac{AD}{DB}=\frac{1}{2}$，则下列结论中正确的是（ ）
如图，在△ABC中，DE∥BC，$\frac{AD}{DB}=\frac{1}{2}$，则下列结论中正确的是（ ）| A． | $\frac{AE}{EC}=\frac{1}{2}$ | B． | $\frac{DE}{BC}=\frac{1}{2}$ | ||
| C． | $\frac{△ADE的周长}{△ABC的周长}=\frac{1}{2}$ | D． | $\frac{△ADE的面积}{△ABC的面积}=\frac{1}{3}$ |