题目内容
19.计算:$\frac{(\sqrt{3}+1)^{2}}{\sqrt{2}}$-($\sqrt{2}+1$)($\sqrt{3}-1$)分析 先利用乘方公式计算得到原式=$\frac{3+2\sqrt{3}+1}{\sqrt{2}}$-($\sqrt{6}$-$\sqrt{2}$+$\sqrt{3}$-1),然后进行分母有理化,再去括号后合并即可.
解答 解:原式=$\frac{3+2\sqrt{3}+1}{\sqrt{2}}$-($\sqrt{6}$-$\sqrt{2}$+$\sqrt{3}$-1)
=2$\sqrt{2}$+$\sqrt{6}$-$\sqrt{6}$+$\sqrt{2}$-$\sqrt{3}$+1
=3$\sqrt{2}$-$\sqrt{3}$+1.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.

练习册系列答案
相关题目
9.小卖部货架上摆放着某品牌方便面,它们的三视图如图,货架上的方便面至多有( )


| A. | 7盒 | B. | 8盒 | C. | 9盒 | D. | 10盒 |
11. 将两个长方体如图放置,则所构成的几何体的左视图可能是( )
将两个长方体如图放置,则所构成的几何体的左视图可能是( )
 将两个长方体如图放置,则所构成的几何体的左视图可能是( )
将两个长方体如图放置,则所构成的几何体的左视图可能是( )| A. |  | B. |  | C. |  | D. |  |
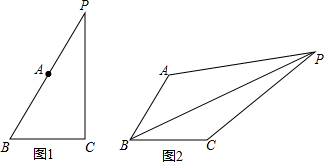
 如图,正方形ABCD中,点O是对角线AC的中点,点P是线段AO上的动点(不与点A、O重合),连结PB,作PE⊥PB交CD于点E.以下结论:①△PBC≌△PDC;②∠PDE=∠PED;③PC-PA=$\sqrt{2}$CE.其中正确的有( )个.
如图,正方形ABCD中,点O是对角线AC的中点,点P是线段AO上的动点(不与点A、O重合),连结PB,作PE⊥PB交CD于点E.以下结论:①△PBC≌△PDC;②∠PDE=∠PED;③PC-PA=$\sqrt{2}$CE.其中正确的有( )个. 安装在屋顶的太阳能热水器的横截面示意图如图所示.已知集热管AE与支架BF所在直线相交于水箱横截面⊙O的圆心O,⊙O的半径为0.2m,AO与屋面AB的夹角为32°,与铅垂线OD的夹角为40°,BF⊥AB于B,OD⊥AD于D,AB=2m,求屋面AB的坡度和支架BF的长.(参考数据:tan18°≈$\frac{1}{3}$,tan32°≈$\frac{31}{50}$,tan40°≈$\frac{21}{25}$)
安装在屋顶的太阳能热水器的横截面示意图如图所示.已知集热管AE与支架BF所在直线相交于水箱横截面⊙O的圆心O,⊙O的半径为0.2m,AO与屋面AB的夹角为32°,与铅垂线OD的夹角为40°,BF⊥AB于B,OD⊥AD于D,AB=2m,求屋面AB的坡度和支架BF的长.(参考数据:tan18°≈$\frac{1}{3}$,tan32°≈$\frac{31}{50}$,tan40°≈$\frac{21}{25}$)