题目内容
15.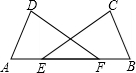 如图,E、F为线段AB上的两点,AF=BE,C、D为线段AB同侧的两点,∠C=∠D,∠A=∠B.
如图,E、F为线段AB上的两点,AF=BE,C、D为线段AB同侧的两点,∠C=∠D,∠A=∠B.求证:AC=BD.
分析 连接AC、BD.由△ADF≌△BCE,推出AD=BC,再证明△ABC≌△BAD即可解决问题.
解答 证明:连接AC、BD.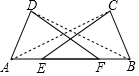
在△ADF和△BCE中,
$\left\{\begin{array}{l}{∠ADC=∠BCE}\\{∠DAF=∠CBE}\\{AF=BE}\end{array}\right.$,
∴△ADF≌△BCE,
∴AD=BC,
在ABC或△BAD中,
$\left\{\begin{array}{l}{AB=BA}\\{∠ABC=∠BAD}\\{BC=AD}\end{array}\right.$,
∴△ABC≌△BAD,
∴AC=BD.
点评 本题考查全等三角形的判定和性质,熟练掌握全等三角形的判定和性质是解题的关键,学会添加常用辅助线,构造全等三角形,属于中考常考题型.

练习册系列答案
相关题目
4. 如图,在平面直角坐标系中,边长为1的正方形OA1B1C1的两边在坐标轴上,以它的对角线OB1,为边作正方形OB1B2C2,再以OB1B2C2正方形的对角线OB2为边作正方形OB2B2C3,依此类推…,则正方形OB99B100C100的顶点B100的坐标是( )
如图,在平面直角坐标系中,边长为1的正方形OA1B1C1的两边在坐标轴上,以它的对角线OB1,为边作正方形OB1B2C2,再以OB1B2C2正方形的对角线OB2为边作正方形OB2B2C3,依此类推…,则正方形OB99B100C100的顶点B100的坐标是( )
 如图,在平面直角坐标系中,边长为1的正方形OA1B1C1的两边在坐标轴上,以它的对角线OB1,为边作正方形OB1B2C2,再以OB1B2C2正方形的对角线OB2为边作正方形OB2B2C3,依此类推…,则正方形OB99B100C100的顶点B100的坐标是( )
如图,在平面直角坐标系中,边长为1的正方形OA1B1C1的两边在坐标轴上,以它的对角线OB1,为边作正方形OB1B2C2,再以OB1B2C2正方形的对角线OB2为边作正方形OB2B2C3,依此类推…,则正方形OB99B100C100的顶点B100的坐标是( )| A. | (2100,0) | B. | (0,250) | C. | (-250,0) | D. | (0,-2100) |
 如图,AB是电线杆,从距离地面12m高的A处,向离电杆5m的B处埋线,并埋入地下1.5m深,求拉线长多少米?
如图,AB是电线杆,从距离地面12m高的A处,向离电杆5m的B处埋线,并埋入地下1.5m深,求拉线长多少米?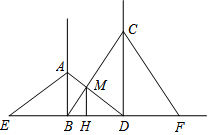 如图,工地上两根电灯杆相距a米,分别在高为4米、6米的A、C处用铁丝将两杆固定,则铁丝AD与铁丝BC的交点M处离地面米的高MH=$\frac{12}{5}$m.
如图,工地上两根电灯杆相距a米,分别在高为4米、6米的A、C处用铁丝将两杆固定,则铁丝AD与铁丝BC的交点M处离地面米的高MH=$\frac{12}{5}$m.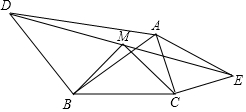 己知:如图,若△ABD和△ACE为等腰Rt△,AB=DB,AC=CE,M为DE中点,求证:△BMC为等腰Rt△.
己知:如图,若△ABD和△ACE为等腰Rt△,AB=DB,AC=CE,M为DE中点,求证:△BMC为等腰Rt△.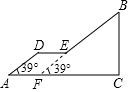 如图,人行天桥的引桥由楼梯和一段水平平台构成,楼梯AD与地面成39°,DE∥AC,楼梯EB与水平地面成39°角,已知BC=6m,AC=11m.
如图,人行天桥的引桥由楼梯和一段水平平台构成,楼梯AD与地面成39°,DE∥AC,楼梯EB与水平地面成39°角,已知BC=6m,AC=11m.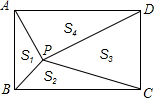 如图,点P是矩形ABCD内一点,连接PA、PB、PC、PD,已知AB=3,BC=4,设△PAB、△PBC、△PCD、△PDA的面积分别为S1、S2、S3、S4,以下判断:
如图,点P是矩形ABCD内一点,连接PA、PB、PC、PD,已知AB=3,BC=4,设△PAB、△PBC、△PCD、△PDA的面积分别为S1、S2、S3、S4,以下判断: