题目内容
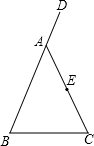 如图,在△ABC中,AB=AC,D是BA延长线上一点,E是AC的中点.
如图,在△ABC中,AB=AC,D是BA延长线上一点,E是AC的中点.(1)利用尺规作出∠DAC的平分线AM,连接BE并延长交AM于点F,(要求在图中标明相应字母,保留作图痕迹,不写作法);
(2)试判断AF与BC有怎样的位置关系与数量关系,并说明理由.
考点:全等三角形的判定与性质,等腰三角形的性质,作图—基本作图
专题:
分析:根据等腰三角形的性质,可得两底角相等,根据三角形的外角的性质,可得∵∠DAC=∠ABC+∠C,根据内错角相等,可得两直线平行,根据ASA,可得两个三角形全等,根据全等三角形的性质,可得证明结论.
解答:解:(1)如图:

(2)AF∥BC且AF=BC
证明:∵AB=AC
∴∠ABC=∠C
∵∠DAC=∠ABC+∠C
∴∠DAC=2∠C
由作图可知∠DAC=2∠FAC
∴∠C=∠FAC
∴AF∥BC;
∵E是AC的中点
∴AE=CE.
在△AEF和△CEB中,
∴△AEF≌△CEB (ASA)
∴AF=BC.

(2)AF∥BC且AF=BC
证明:∵AB=AC
∴∠ABC=∠C
∵∠DAC=∠ABC+∠C
∴∠DAC=2∠C
由作图可知∠DAC=2∠FAC
∴∠C=∠FAC
∴AF∥BC;
∵E是AC的中点
∴AE=CE.
在△AEF和△CEB中,
|
∴△AEF≌△CEB (ASA)
∴AF=BC.
点评:本题考查了全等三角形的性质与判定,利用三角形的外角的性质,角平分线的性质,平行线的判定,全等三角形的判定解题是解题关键.

练习册系列答案
相关题目
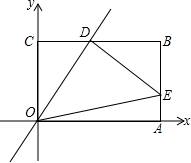 如图,在平面直角坐标系中,矩形OABC的顶点A在x轴上,点C在y轴上,点B的坐标是(8,6),正比例函数y=kx的图象交BC于点D,DE⊥OD,交AB于点E,连结OE.
如图,在平面直角坐标系中,矩形OABC的顶点A在x轴上,点C在y轴上,点B的坐标是(8,6),正比例函数y=kx的图象交BC于点D,DE⊥OD,交AB于点E,连结OE. 已知:如图,在平面直角坐标系xOy中,点A(2
已知:如图,在平面直角坐标系xOy中,点A(2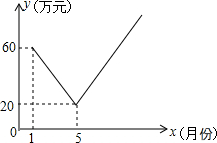 保护生态环境,实行“节能减排”的理念已深入人心.我市某工厂从2014年1月开始,进行机器设备更新,产业转型换代的改造,改造期间利润明显下降,从1月份利润60万元逐月等额下降,到5月份利润为20万元;5月底改造完成,从这时起,该厂每个月的利润都比上个月增加15万元.设第x个月的利润为y(万元),函数图象如图.
保护生态环境,实行“节能减排”的理念已深入人心.我市某工厂从2014年1月开始,进行机器设备更新,产业转型换代的改造,改造期间利润明显下降,从1月份利润60万元逐月等额下降,到5月份利润为20万元;5月底改造完成,从这时起,该厂每个月的利润都比上个月增加15万元.设第x个月的利润为y(万元),函数图象如图. 如图,防水堤坝的轴截面是等腰梯形ABCD,DA=CB,DC∥AB,DA=5,DC=4,AB=9,则斜坡DA的坡角为
如图,防水堤坝的轴截面是等腰梯形ABCD,DA=CB,DC∥AB,DA=5,DC=4,AB=9,则斜坡DA的坡角为