题目内容
在平面直角坐标系中,点A的坐标为(3,0),点B为y轴正半轴上的一点,点C为第一象限内一点,且AC=2,设tan∠BOC=m,则m的取值范围是( )
| A、m≥0 | ||||
B、m≥
| ||||
C、m≤
| ||||
D、0≤m≤
|
考点:直线与圆的位置关系,坐标与图形性质,锐角三角函数的定义
专题:
分析:C在以A为圆心,以2为半径的圆周上,只有当OC与圆A相切(即到C点)时,∠BOC最小,根据勾股定理求出此时的OC,求出∠BOC=∠CAO,根据解直角三角形求出此时的值,根据tan∠BOC的增减性,即可求出答案.
解答:解:C在以A为圆心,以2为半径作圆周上,只有当OC与圆A相切(即到C点)时,∠BOC最小,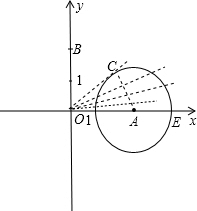
AC=2,OA=3,由勾股定理得:OC=
,
∵∠BOA=∠ACO=90°,
∴∠BOC+∠AOC=90°,∠CAO+∠AOC=90°,
∴∠BOC=∠OAC,
tan∠BOC=tan∠OAC=
=
,
随着C的移动,∠BOC越来越大,
∵C在第一象限,
∴C不到x轴点,
即∠BOC<90°,
∴tan∠BOC≥
,
故选B.

AC=2,OA=3,由勾股定理得:OC=
| 5 |
∵∠BOA=∠ACO=90°,
∴∠BOC+∠AOC=90°,∠CAO+∠AOC=90°,
∴∠BOC=∠OAC,
tan∠BOC=tan∠OAC=
| OC |
| AC |
| ||
| 2 |
随着C的移动,∠BOC越来越大,
∵C在第一象限,
∴C不到x轴点,
即∠BOC<90°,
∴tan∠BOC≥
| ||
| 2 |
故选B.
点评:本题考查了解直角三角形,勾股定理,切线的性质等知识点的应用,能确定∠BOC的变化范围是解此题的关键,题型比较好,但是有一定的难度.

练习册系列答案
相关题目
 △ABC中,DE∥BC,EF∥AB,则与∠ADE不一定相等的是( )
△ABC中,DE∥BC,EF∥AB,则与∠ADE不一定相等的是( )| A、∠B | B、∠EFC |
| C、∠A | D、∠ADE |
在平面直角坐标系中,对于坐标P(2,5),下列说法错误的是( )
| A、P(2,5)表示这个点在平面内的位置 |
| B、点P的纵坐标是:5 |
| C、点P到x轴的距离是5 |
| D、它与点(5,2)表示同一个坐标 |
下列说法中:
①一组对角相等;②两条对角线互相垂直;③两条对角线互相平分;④一组邻角互补;⑤两组对边都相等;⑥两组对边分别平行.
这些说法中能判定四边形是平行四边形的有( )个.
①一组对角相等;②两条对角线互相垂直;③两条对角线互相平分;④一组邻角互补;⑤两组对边都相等;⑥两组对边分别平行.
这些说法中能判定四边形是平行四边形的有( )个.
| A、5 | B、4 | C、3 | D、2 |
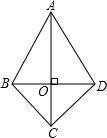 如图,四边形ABCD中,∠BCD=90°,BC=CD,对角线AC⊥BD于点O,若AD=
如图,四边形ABCD中,∠BCD=90°,BC=CD,对角线AC⊥BD于点O,若AD=| 2 |
| A、100° | B、105° |
| C、85° | D、95° |
 如图,⊙O的半径OA,OB,且OA⊥OB,连结AB.现在⊙O上找一点C,使OA2+AB2=BC2,则∠OAC的度数为( )
如图,⊙O的半径OA,OB,且OA⊥OB,连结AB.现在⊙O上找一点C,使OA2+AB2=BC2,则∠OAC的度数为( )| A、15°或75° |
| B、20°或70° |
| C、20° |
| D、30° |
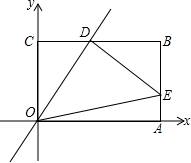 如图,在平面直角坐标系中,矩形OABC的顶点A在x轴上,点C在y轴上,点B的坐标是(8,6),正比例函数y=kx的图象交BC于点D,DE⊥OD,交AB于点E,连结OE.
如图,在平面直角坐标系中,矩形OABC的顶点A在x轴上,点C在y轴上,点B的坐标是(8,6),正比例函数y=kx的图象交BC于点D,DE⊥OD,交AB于点E,连结OE.