题目内容
通讯商城计划用32400元购进一批智能手机,A、B、C三种型号共15台,三种手机的进价和售价如下表:
(1)在不超过现有资金的前提下,若购进A型手机的数量与B型的数量相同,C型手机的数量不大于A型数量的一半,商场有几种进货方案?
(2)某公司因为工作需要,给员工购买手机,商场按团价打9折,将15台手机全部卖给他们,公司能节省多少元?
 |
进价(元/台) | 售价(元/台) |
| A | 2000 | 2100 |
| B | 2400 | 2500 |
| C | 1600 | 1700 |
(2)某公司因为工作需要,给员工购买手机,商场按团价打9折,将15台手机全部卖给他们,公司能节省多少元?
考点:一元一次不等式的应用
专题:
分析:(1)设购进A型和B型的手机为x台,则购进C型手机为(15-2x)台,根据C型手机的数量不大于A型数量的一半,进货价不超过32400元,列不等式组求解;
(2)根据(1)中求出的不同进货方案,求出该公司能节省的钱数.
(2)根据(1)中求出的不同进货方案,求出该公司能节省的钱数.
解答:解:(1)设购进A型和B型的手机为x台,则购进C型手机为(15-2x)台,
由题意得,
,
解①得:x≥6,
解②得:x≤7,
则进货方案有:A型和B型各6台,C型3台;
A型和B型各7台,C型1台;
(2)①当该公司购买A型和B型各6台,C型3台时,
节省:[2100×6+2500×6+1700×3]×0.1=3270(元);
②当该公司购买A型和B型各7台,C型1台时,
节省:[2100×7+2500×7+1700]×0.1=3390(元).
答:该公司若是购买A型和B型各6台,C型3台,节省3270元;该公司若是购买A型和B型各7台,C型1台,节省3390元.
由题意得,
|
解①得:x≥6,
解②得:x≤7,
则进货方案有:A型和B型各6台,C型3台;
A型和B型各7台,C型1台;
(2)①当该公司购买A型和B型各6台,C型3台时,
节省:[2100×6+2500×6+1700×3]×0.1=3270(元);
②当该公司购买A型和B型各7台,C型1台时,
节省:[2100×7+2500×7+1700]×0.1=3390(元).
答:该公司若是购买A型和B型各6台,C型3台,节省3270元;该公司若是购买A型和B型各7台,C型1台,节省3390元.
点评:此题主要考查了一元一次不等式组的应用,解决问题的关键是读懂题意,找到关键描述语,进而找到所求的量的等量关系.

练习册系列答案
相关题目
在平面直角坐标系中,对于坐标P(2,5),下列说法错误的是( )
| A、P(2,5)表示这个点在平面内的位置 |
| B、点P的纵坐标是:5 |
| C、点P到x轴的距离是5 |
| D、它与点(5,2)表示同一个坐标 |
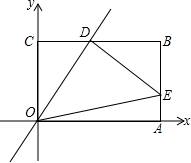 如图,在平面直角坐标系中,矩形OABC的顶点A在x轴上,点C在y轴上,点B的坐标是(8,6),正比例函数y=kx的图象交BC于点D,DE⊥OD,交AB于点E,连结OE.
如图,在平面直角坐标系中,矩形OABC的顶点A在x轴上,点C在y轴上,点B的坐标是(8,6),正比例函数y=kx的图象交BC于点D,DE⊥OD,交AB于点E,连结OE.