题目内容
4．
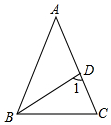如图，在△ABC中，AB=AC，∠BAC=36°，BD平分∠ABC，则∠1的度数是72°．
分析 由已知根据等腰三角形的性质易得两底角的度数，结合角平分线的性质和三角形内角和定理即可求解．
解答 解：∵AB=AC，∠A=36°，
∴∠ABC=∠C=（180°-36°）÷2=72°，
又∵BD为∠ABC的平分线，
∴∠ABD=36°，
∴∠1=72°，
故答案为：72°．
点评 本题考查了三角形内角和定理及等腰三角形的性质、角平分线的性质；综合运用各种知识是解答本题的关键．
练习册系列答案
相关题目
6．已知，3＜m＜6，且点A（m，y1），B（$\frac{1}{3}$m+1，y2），C（2，y3）都在二次函数y=$\sqrt{5}$x2-2$\sqrt{5}$x+3的图象上，则下列说法正确的是（ ）
| A． | y2＜y1＜y3 | B． | y2＜y3＜y1 | C． | y3＜y2＜y1 | D． | y1＜y3＜y2 |
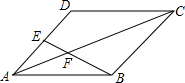已知平行四边形ABCD中，点E为AD的中点，连接BE交AC于点F．求AF：CF的值．
如图，已知抛物线与x轴交于A（-1，0）、B（5，0）两点，与y轴交于点C（0，5）．
16．已知等腰△两条边的长分别是3和6，则它的周长是（ ）
| A． | 12 | B． | 15 | C． | 12或15 | D． | 15或18 |
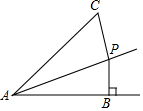如图，点P是∠BAC的平分线上一点，PB⊥AB于B，且PB=5，AC=12，则△APC的面积是30．