题目内容
13．
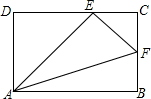如图，在矩形ABCD中，E、F分别是DC、BC边上的点，且∠AEF=90°则下列结论正确的是（ ）| A． | △ABF∽△AEF | B． | △ABF∽△CEF | C． | △CEF∽△DAE | D． | △DAE∽△BAF |
分析 利用等角的余角相等可得∠DAE=∠CEF，加上∠D=∠C=90°，则根据有两组角对应相等的两个三角形相似可判断△CEF∽△DAE．
解答 解：∵∠AEF=90°，
∴∠ADE+∠CEF=90°，
而∠ADE+∠DAE=90°，
∴∠DAE=∠CEF，
而∠D=∠C=90°，
∴△CEF∽△DAE．
故选C．
点评 本题考查了相似三角形的判定：有两组角对应相等的两个三角形相似．也考查了矩形的性质．
练习册系列答案
学练快车道口算心算速算天天练系列答案
相关题目
3．化简：$\sqrt{\frac{{x}^{2}y}{x}}$•$\sqrt{xy}$=（ ）
| A． | xy | B． | y | C． | x | D． | x$\sqrt{y}$ |
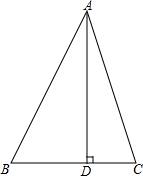如图，△ABC中，∠A=45°，过点A作AD⊥BC，BD=2，BC=3，求S△ABC．
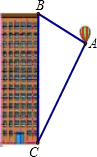如图，热气球的探测器显示，从热气球看一栋高楼顶部的仰角为35.6°，看这栋高楼底部的俯角的正切值为2，热气球与高楼的水平距离为90米，这栋高楼有多高（结果精确到0.1米．参考数据：sin35.6°=0.582，cos35.6°=0.813，tan35.6°=0.716）？
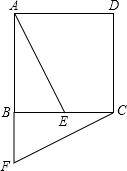如图，正方形ABCD中，E为BC边上的一点，将△ABE旋转后得到△CBF．