题目内容
2. 如图,四边形ABCD和四边形ACED都是平行四边形,点R在DE上,且DR:RE=5:4,BR分别与AC、CD相交于点P、Q,则BP:PQ:QR=7:2:5.
如图,四边形ABCD和四边形ACED都是平行四边形,点R在DE上,且DR:RE=5:4,BR分别与AC、CD相交于点P、Q,则BP:PQ:QR=7:2:5.
分析 用平行四边形的性质得到平行,可得到PB=PR,$\frac{PC}{RE}=\frac{1}{2}$,且DR:RE=5:4,代入可得到QR和PQ之间的关系,结合BP=PR=PQ+QR=$\frac{7}{2}$PQ,可得到答案.
解答 解:∵四边形ABCD和四边形ACED都是平行四边形,
∴BC=AD=CE,AC∥DE,
∴PB=PR,$\frac{PC}{RE}=\frac{1}{2}$,
又∵PC∥DR,
∴△PCQ∽△RDQ,
∴$\frac{PQ}{QR}=\frac{PC}{DR}$,
∵DR:RE=5:4,
∴RE=$\frac{4}{5}$DR,
∴$\frac{PQ}{QR}=\frac{PC}{DR}$=$\frac{2}{5}$,
∴QR=$\frac{5}{2}$PQ,
又∵BP=PR=PQ+QR=$\frac{7}{2}$PQ,
∴BP:PQ:QR=7:2:5,
故答案为:7:2:5.
点评 本题主要考查平行线分线段成比例的性质及平行四边形的性质,由条件得到QR=$\frac{5}{2}$PQ,BP=$\frac{7}{2}$PQ,是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.一队学生去校外进行训练,他们以5千米/时的速度行进,走了18分的时候,学校要将一个紧急通知传给队长,通讯员从学校出发,骑自行车以14千米/时的速度按原路追上去,通讯员需多少时间可以追上学生队伍?
10.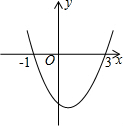 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有如下结论:
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有如下结论:
①a>0;②b>0;③a+b+c>0;④2a+b=0;⑤方程ax2+bx+c=0的解为x1=-1,x2=3.
其中正确的是( )
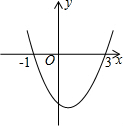 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有如下结论:
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有如下结论:①a>0;②b>0;③a+b+c>0;④2a+b=0;⑤方程ax2+bx+c=0的解为x1=-1,x2=3.
其中正确的是( )
| A. | ①②③ | B. | ②③④ | C. | ③④⑤ | D. | ①④⑤ |
17. 如图,在△ABC中,点D、E分别是AB、C的中点,则S△ADE:S△ABC=( )
如图,在△ABC中,点D、E分别是AB、C的中点,则S△ADE:S△ABC=( )
 如图,在△ABC中,点D、E分别是AB、C的中点,则S△ADE:S△ABC=( )
如图,在△ABC中,点D、E分别是AB、C的中点,则S△ADE:S△ABC=( )| A. | 1:2 | B. | 1:3 | C. | 1:4 | D. | 1:5 |
11. 为了解某校九年级学生中考体育测试成绩,现从中随机抽取部分学生的中考体育成绩进行分段(A等:90~100分;B等:75~89分;C等:60~74分;D等:60分以下)统计如下:
为了解某校九年级学生中考体育测试成绩,现从中随机抽取部分学生的中考体育成绩进行分段(A等:90~100分;B等:75~89分;C等:60~74分;D等:60分以下)统计如下:
请你根据以上图表提供的信息,解答下列问题:
(1)x=0.38,n=8;
(2)在扇形统计图中,B等级所对应的扇形圆心角是144度;
(3)如果把成绩在60分以上(含60分)定为合格,若该校九年级共有500名学生参加了本次中考体育测试,那么请你估计成绩为合格的学生人数约有多少名?
 为了解某校九年级学生中考体育测试成绩,现从中随机抽取部分学生的中考体育成绩进行分段(A等:90~100分;B等:75~89分;C等:60~74分;D等:60分以下)统计如下:
为了解某校九年级学生中考体育测试成绩,现从中随机抽取部分学生的中考体育成绩进行分段(A等:90~100分;B等:75~89分;C等:60~74分;D等:60分以下)统计如下:| 等级 | 成绩(分) | 频数(人数) | 频率 |
| A | 90~100 | 19 | x |
| B | 75~89 | 20 | 0.4 |
| C | 60~74 | n | 0.16 |
| D | 60以下 | 3 | 0.06 |
| 合计 | 50 | 1.00 |
(1)x=0.38,n=8;
(2)在扇形统计图中,B等级所对应的扇形圆心角是144度;
(3)如果把成绩在60分以上(含60分)定为合格,若该校九年级共有500名学生参加了本次中考体育测试,那么请你估计成绩为合格的学生人数约有多少名?
 如图,将三角形ABC沿射线BC的方向平移到三角形A′B′C′的位置,AC与A′B′相交于点M,请找出一对面积相等的图形.
如图,将三角形ABC沿射线BC的方向平移到三角形A′B′C′的位置,AC与A′B′相交于点M,请找出一对面积相等的图形. 如图,点A,B,C,D在同一直线上,AB=CD,AE∥CF且AE=CF,求证:BE=DF.
如图,点A,B,C,D在同一直线上,AB=CD,AE∥CF且AE=CF,求证:BE=DF.