题目内容
11．一个三位数，从百位到个位的数字依次由三个连续奇数从小到大组成，若把百位数字与个位数字对调，则所得到的新数比原数的二倍还大39，求原来的三位数．分析 设百位数字是a，则十位数字是（a+2），个位数字是（a+4）．依据“把百位数字与个位数字对调，则所得到的新数比原数的二倍还大39”列出方程并解答．
解答 解：设百位数字是a，则十位数字是（a+2），个位数字是（a+4）．
依题意得2[100a+10（a+2）+（a+4）]+39=100（a+4）+10（a+2）+a．
解得a=3，
则原来的三位数是357．
答：原来的三位数是357．
点评 本题考查了一元一次方程的应用．解题关键是要读懂题目的意思，根据题目给出的条件，找出合适的等量关系列出方程，再求解．
练习册系列答案
相关题目
1．
如图是某商场一楼与二楼之间的手扶电梯示意图，其中AB、CD分别表示一楼、二楼地面的水平线，∠ABC=150°，如果顾客乘地铁从点B到点C上升的高度为5m，则电梯BC的长是（ ）
如图是某商场一楼与二楼之间的手扶电梯示意图，其中AB、CD分别表示一楼、二楼地面的水平线，∠ABC=150°，如果顾客乘地铁从点B到点C上升的高度为5m，则电梯BC的长是（ ）| A． | 5cm | B． | 5$\sqrt{3}$cm | C． | 10m | D． | $\frac{10\sqrt{3}}{3}$m |
11．
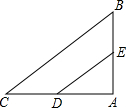如图，△ABC中，AB=3，AC=4，BC=5，D、E分别是AC、AB的中点，则以DE为直径的圆与BC的位置关系是（ ）
如图，△ABC中，AB=3，AC=4，BC=5，D、E分别是AC、AB的中点，则以DE为直径的圆与BC的位置关系是（ ）| A． | 相切 | B． | 相交 | C． | 相离 | D． | 无法确定 |