题目内容
10.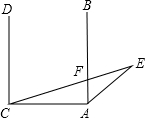 如图,AB⊥AC,DC⊥AC,∠ECD=75°,∠EAB:∠E=3:2,求∠E的度数.
如图,AB⊥AC,DC⊥AC,∠ECD=75°,∠EAB:∠E=3:2,求∠E的度数.
分析 先根据题意得出AB∥CD,再由平行线的性质得出∠BFE=∠DCE,再设∠EAB=3x,则∠E=2x,由三角形外角的性质即可得出x的值,进而可得出结论.
解答 解:∵AB⊥AC,DC⊥AC,∠ECD=75°,
∴AB∥CD.
∴∠BFE=∠DCE=75°.
∵∠EAB:∠E=3:2,
∴设∠EAB=3x,则∠E=2x.
∵∠BFE是△AEF的外角,
∴∠BFE=∠EAB+∠E=3x+2x=5x=75°,
∴x=15°,
∴∠E=2x=30°.
点评 本题考查的是平行线的判定与性质,熟知平行线的判定定理是解答此题的关键.

练习册系列答案
相关题目
20.从二次根式$\sqrt{12}$、$\sqrt{{x}^{2}+3}$、$\sqrt{\frac{3}{2}}$、$\sqrt{{a}^{2}b}$、2$\sqrt{0.5}$、$\sqrt{26}$中任选一个,不是最简二次根式的概率是( )
| A. | $\frac{1}{6}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
5.分式方程$\frac{3}{2x}$=$\frac{1}{x-1}$的解为( )
| A. | x=1 | B. | x=2 | C. | x=-3 | D. | x=3 |
15.下列长度的线段不能构成直角三角形的是( )
| A. | 6,8,10 | B. | 5,12,13 | C. | 1.5,2,3 | D. | $\sqrt{2}$,$\sqrt{11}$,3 |
2.若单项式-2am+2b与5ab2m+n是同类项,则mn的值是( )
| A. | 1 | B. | -1 | C. | 16 | D. | -32 |
20. AB为⊙O的直径,点C、D在⊙O上.若∠ABD=42°,则∠BCD的度数是( )
AB为⊙O的直径,点C、D在⊙O上.若∠ABD=42°,则∠BCD的度数是( )
 AB为⊙O的直径,点C、D在⊙O上.若∠ABD=42°,则∠BCD的度数是( )
AB为⊙O的直径,点C、D在⊙O上.若∠ABD=42°,则∠BCD的度数是( )| A. | 122° | B. | 132° | C. | 128° | D. | 138° |