题目内容
20. AB为⊙O的直径,点C、D在⊙O上.若∠ABD=42°,则∠BCD的度数是( )
AB为⊙O的直径,点C、D在⊙O上.若∠ABD=42°,则∠BCD的度数是( )| A. | 122° | B. | 132° | C. | 128° | D. | 138° |
分析 连接AD,根据圆周角定理可得∠ADB=90°,然后可得∠DAB=48°,再根据圆内接四边形对角互补可得答案.
解答  解:连接AD,
解:连接AD,
∵AB为⊙O的直径,
∴∠ADB=90°,
∵∠ABD=42°,
∴∠DAB=48°,
∴∠BCD=180°-48°=132°,
故选:B.
点评 此题主要考查了圆周角定理和圆内接四边形的性质,关键是掌握半圆(或直径)所对的圆周角是直角.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
8.若a>0且ax=2,ay=3,则ax-y的值为( )
| A. | 6 | B. | 5 | C. | -1 | D. | $\frac{2}{3}$ |
15.36的平方根是( )
| A. | ±6 | B. | ±18 | C. | 6 | D. | -6 |
5.下列各式中正确的是( )
| A. | -3.14<-π | B. | -(-3)>|-2| | C. | -(-3)2>-(-2)3 | D. | (x+1)2>0 |
10.如图是一个简单的数值运算程序,当输入的x的值为2时,则输出的值为( )


| A. | 6 | B. | -8 | C. | 8 | D. | -6 |
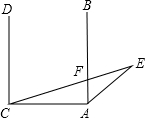 如图,AB⊥AC,DC⊥AC,∠ECD=75°,∠EAB:∠E=3:2,求∠E的度数.
如图,AB⊥AC,DC⊥AC,∠ECD=75°,∠EAB:∠E=3:2,求∠E的度数.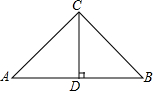 如图:在等腰直角△ABC中,CA=CB,CD⊥AB于D,AB=10,则CD=5.
如图:在等腰直角△ABC中,CA=CB,CD⊥AB于D,AB=10,则CD=5. 如图,△ABC中,∠A=25°,∠B=70°,CE平分∠ACB,CD⊥AB于点D,DF⊥CE于点F,则∠EDF=22.5°.
如图,△ABC中,∠A=25°,∠B=70°,CE平分∠ACB,CD⊥AB于点D,DF⊥CE于点F,则∠EDF=22.5°.