题目内容
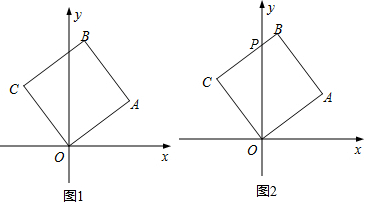
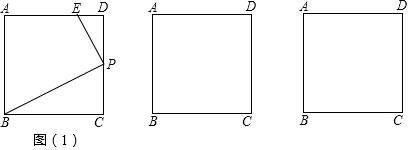
14.操作:正方形ABCD的边长为4,P是直线CD上一动点,将三角尺的直角顶点与点P重合,一条直角边始终经过点B,另一直角边所在的直线与射线AD交于点E,设CP=x,DE=y.探究:(1)如图(1),当点P在正方形ABCD的边CD上时,求证:△BPC∽△PED;
(2)当点P在CD的延长线上时,求y关于x的函数关系式;
(3)当DE=1时,求点P的位置.
分析 (1)证根据余角的性质得到∠DPE=∠BPC,根据相似三角形的判定定理即可得到结论;
(2)根据相似三角形的性质得到$\frac{PD}{BC}$=$\frac{DE}{CP}$,代入数据即可得到结论;
(3)当点P在正方形ABCD的边CD上时,如图1,根据相似三角形的性质得到CP=2,当点P在CD的延长线上时,如图2,列方程求得结果.
解答 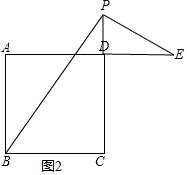 (1)证明:∵∠EPB=90°,
(1)证明:∵∠EPB=90°,
∴∠BPC+∠DPE=90°
∵∠PBC+∠BPC=90°,
∴∠DPE=∠BPC,
∵∠D=∠C,
∴△BPC∽△PED;
(2)解:∵∠EPB=90°,
∴∠BPC+∠DPE=90°
∵∠PBC+∠BPC=90°,
∴∠DPE=∠BPC,
∵∠PDE=∠BCP,
∴△BPC∽△PED,
∴$\frac{PD}{BC}$=$\frac{DE}{CP}$,
∵CP=x,DE=y,BC=CD=4,
∴PD=x-4,
∴$\frac{x-4}{4}$=$\frac{y}{x}$,
∴y=$\frac{{x}^{2}}{4}$-x;
(3)解:当点P在正方形ABCD的边CD上时,如图1,△BPC∽△PED,
∴$\frac{DE}{CP}$=$\frac{DP}{BC}$,
∴$\frac{1}{CP}$=$\frac{4-CP}{4}$,
∴CP=2,
当点P在CD的延长线上时,如图2,DE=y=1,
∴$\frac{{x}^{2}}{4}$-x=1,
解得:x=2±2$\sqrt{2}$,
由于CP=x>4,
即CP=2+2$\sqrt{2}$.
点评 此题主要考查了求函数解析式,相似三角形的判定与性质以及分类讨论思想的应用,根据已知得出不同图形进行讨论得出是解题关键.

练习册系列答案
相关题目
4.已知$\left\{{\begin{array}{l}{x=2}\\{y=3}\end{array}}\right.$是关于x、y的方程4kx-3y=-1的一个解,则k的值为( )
| A. | 1 | B. | -1 | C. | 2 | D. | -2 |
5.若点P在第二象限内,且到x轴的距离是5,到y轴的距离是7,则点P的坐标是( )
| A. | (-7,5) | B. | (7,-5) | C. | (-5,7) | D. | (5,-7) |
10.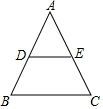 如图,在△ABC中,AB=AC,DE∥BC,则下列结论中,不正确的是( )
如图,在△ABC中,AB=AC,DE∥BC,则下列结论中,不正确的是( )
 如图,在△ABC中,AB=AC,DE∥BC,则下列结论中,不正确的是( )
如图,在△ABC中,AB=AC,DE∥BC,则下列结论中,不正确的是( )| A. | AD=AE | B. | DE=$\frac{1}{2}$EC | C. | ∠ADE=∠C | D. | DB=EC |
 如图,在4×4的正方形网格中,已将四个小正方形涂上阴影,有一个小虫落到网格中,那么小虫落到阴影部分的概率是$\frac{1}{4}$.
如图,在4×4的正方形网格中,已将四个小正方形涂上阴影,有一个小虫落到网格中,那么小虫落到阴影部分的概率是$\frac{1}{4}$.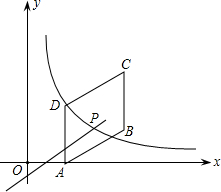 如图,四边形ABCD是平行四边形,点A(1,0),B(4,1),C(4,3),反比例函数y=$\frac{k}{x}$的图象经过点D,点P是一次函数y=mx+3-4m(m≠0)的图象与该反比例函数图象的一个公共点;
如图,四边形ABCD是平行四边形,点A(1,0),B(4,1),C(4,3),反比例函数y=$\frac{k}{x}$的图象经过点D,点P是一次函数y=mx+3-4m(m≠0)的图象与该反比例函数图象的一个公共点;