题目内容
已知：如图，在△ABC中．O是∠ABC、∠CAB外角的平分线的交点，那么点O在∠C的平分线上吗？为什么？考点：角平分线的性质
专题：
分析：过点O作OD⊥AB于D，作OE⊥AC于E，作OF⊥BC于F，根据角平分线上的点到角的两边距离相等可得OF=OD=OE，再根据到角的两边距离相等的点在角的平分线上解答．
解答：
解：点O在∠C的平分线上．
理由如下：O作OD⊥AB于D，作OE⊥AC于E，作OF⊥BC于F，
∵O是∠ABC和∠CAB外角的平分线的交点，
∴OD=OF，OE=OF，
∴OF=OD=OE，
∴点O在∠C的平分线上．
解：点O在∠C的平分线上．理由如下：O作OD⊥AB于D，作OE⊥AC于E，作OF⊥BC于F，
∵O是∠ABC和∠CAB外角的平分线的交点，
∴OD=OF，OE=OF，
∴OF=OD=OE，
∴点O在∠C的平分线上．
点评：本题考查了角平分线上的点到角的两边距离相等的性质，到角的两边距离相等的点在角的平分线上，作出辅助线并熟记性质与定理是解题的关键．
练习册系列答案
相关题目
如图，∠B=∠D=90°，根据角平分线性质，填空：
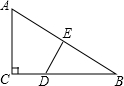如图所示，Rt△ABC中，∠C=90°，AB的垂直平分线DE交BC于点D，交AB于点E．当∠B=30°时，下列结论不正确的是（ ）| A、AC=AE=BE |
| B、AD=BD |
| C、CD=BD |
| D、CE=BE |
如图所示，如果只给你一把带有刻度的直尺，你是否能检验∠MPN是不是直角？简述你的作法，并说明理由．二次函数的图象经过（0，3），（-2，-5），（1，4）三点，则它的解析式为（ ）
| A、y=x2+6x+3 |
| B、y=-3x2-2x+3 |
| C、y=2x2+8x+3 |
| D、y=-x2+2x+3 |