题目内容
已知：如图，在△ABC中，边AB，BC的垂直平分线交于P．求证：PA=PB=PC．考点：线段垂直平分线的性质
专题：证明题
分析：直接根据线段垂直平分线的性质即可得出结论．
解答：证明：∵点P是边AB，BC的垂直平分线的交点，
∴PA=PB，PB=PC，
∴PA=PB=PC．
∴PA=PB，PB=PC，
∴PA=PB=PC．
点评：本题考查的是线段垂直平分线的性质，熟知线段垂直平分线上任意一点，到线段两端点的距离相等是解答此题的关键．
练习册系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
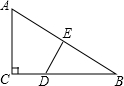如图所示，Rt△ABC中，∠C=90°，AB的垂直平分线DE交BC于点D，交AB于点E．当∠B=30°时，下列结论不正确的是（ ）| A、AC=AE=BE |
| B、AD=BD |
| C、CD=BD |
| D、CE=BE |
二次函数的图象经过（0，3），（-2，-5），（1，4）三点，则它的解析式为（ ）
| A、y=x2+6x+3 |
| B、y=-3x2-2x+3 |
| C、y=2x2+8x+3 |
| D、y=-x2+2x+3 |
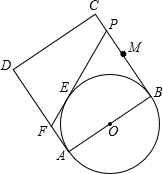已知正方形ABCD的边长为2，点M是BC的中点，P是线段MC上的一个动点，P不与M和C重合，以AB为直径作⊙O，过点P作⊙O的切线交AD于点F，切点为E．求四边形CDFP的周长．
如图，在△ABC中，AB=AC=20cm，DE垂直平分AB，垂足为E，交AC于D，若△DBC的周长为35cm，则BC的长为（ ）| A、5cm | B、10cm |
| C、15cm | D、17.5cm |
下列因式分解错误的是（ ）
| A、x2-4y2=（x+2y）（x-2y） |
| B、x2-6xy+9y2=（x-3y）2 |
| C、x2+xy=x（x+y） |
| D、x2-y2=（x+y）2 |