题目内容
 已知:正方形ABCD中,BE=CF,AE、AF的垂线相交于点P,连接EF、CP.求证:CP⊥EF.
已知:正方形ABCD中,BE=CF,AE、AF的垂线相交于点P,连接EF、CP.求证:CP⊥EF.考点:正方形的性质,相似三角形的判定与性质
专题:证明题
分析:连接BF,DE,EF,做PG⊥CB,PH⊥CD,证得△ABE≌△BCF,△PEG∽△FBC,△PFH∽△EDC,进一步推出△PGC∽△FCE,进一步证得结论即可.
解答:解:连接BF,DE,EF,做PG⊥CB,PH⊥CD,

在△ABE和△BCF中,
,
∴△ABE≌△BCF(SAS),
∴∠FBC=∠BAE,
∵∠BAE+∠AEB=90°,
∴∠FBC+∠AEB=90°,即AE⊥BF,
∵EP⊥AE,
∴EP∥BF,
∵PG⊥CB,CF⊥CB,
∴△PEG∽△FBC,
设BE=X=CF,CE=DF=Y
PG:X=(Y-CG):(X+Y) ①
同理得
△PFH∽△EDC,
(Y-EG):Y=(X-PG):(X+Y) ②
由①②得
PG:CG=Y:X,
∵∠PGC=∠DCB,
∴△PGC∽△FCE,
∴∠PCG=∠EFC,
∵∠FEC+∠EFC=90°,
∠FEC+∠PCG=90°,
∴CP⊥EF.

在△ABE和△BCF中,
|
∴△ABE≌△BCF(SAS),
∴∠FBC=∠BAE,
∵∠BAE+∠AEB=90°,
∴∠FBC+∠AEB=90°,即AE⊥BF,
∵EP⊥AE,
∴EP∥BF,
∵PG⊥CB,CF⊥CB,
∴△PEG∽△FBC,
设BE=X=CF,CE=DF=Y
PG:X=(Y-CG):(X+Y) ①
同理得
△PFH∽△EDC,
(Y-EG):Y=(X-PG):(X+Y) ②
由①②得
PG:CG=Y:X,
∵∠PGC=∠DCB,
∴△PGC∽△FCE,
∴∠PCG=∠EFC,
∵∠FEC+∠EFC=90°,
∠FEC+∠PCG=90°,
∴CP⊥EF.
点评:此题考查正方形的性质,三角形全等的判定与性质,三角形相似的判定与性质,注意结合图形,理清思路,解决问题.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
下列不等式组无解的是( )
A、
| |||||
B、
| |||||
C、
| |||||
D、
|
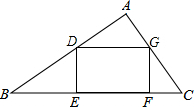 在△ABC中,BC=10,S△ABC=30,矩形DEFG内接于△ABC,设DE=x,S矩形DEFG=y.求:
在△ABC中,BC=10,S△ABC=30,矩形DEFG内接于△ABC,设DE=x,S矩形DEFG=y.求: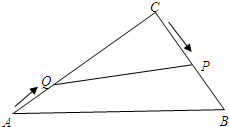 已知:如图,在△ABC中,∠C=Rt∠,AB=10cm,BC=6cm,点P从点C开始沿边CB以2cm/s的速度向点B移动,与此同时,点Q从点A开始沿边AC以1cm/s的速度向点C移动,两点同时出发,当其中一点到达终点时,另一点也随之停止移动.若设移动时间为t秒.
已知:如图,在△ABC中,∠C=Rt∠,AB=10cm,BC=6cm,点P从点C开始沿边CB以2cm/s的速度向点B移动,与此同时,点Q从点A开始沿边AC以1cm/s的速度向点C移动,两点同时出发,当其中一点到达终点时,另一点也随之停止移动.若设移动时间为t秒.