题目内容
已知函数y=x2-5x-14,作出函数图象并求其与x轴的交点坐标.
考点:二次函数的图象,抛物线与x轴的交点
专题:作图题
分析:先把解析式配成顶点式,再进行列表、描点、连线画抛物线,然后观察函数图象得抛物线与x轴的交点坐标.
解答:解:y=(x-
)2-
,
列表
描点:如图,
连线,如图,
抛物线与y轴的交点坐标为(-2,0)和(7,0).
| 5 |
| 2 |
| 81 |
| 4 |
列表
| X | … | -2 | 0 | 2.5 | 5 | 7 | … |
| Y | … | 0 | -14 | -20.25 | -14 | 0 | … |
连线,如图,

抛物线与y轴的交点坐标为(-2,0)和(7,0).
点评:本题考查了二次函数的图象:二次函数y=ax2+bx+c(a≠0)的图象为抛物线,先把抛物线的解析式配成顶点式,再利用列表、描点和连线画二次函数图象.也考查了抛物线与x轴的交点.

练习册系列答案
相关题目
若x1,x2是一元二次方程x2-x-1=0的两根,则x1x2的值是( )
| A、1 | ||
| B、-1 | ||
C、
| ||
D、-
|
下列运算正确的是( )
| A、a+b-(a-b)=0 | ||||||
B、5
| ||||||
| C、(m-1)(m+2)=m2-m+2 | ||||||
| D、(-1)2010-1=2009 |
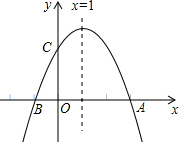 如图,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A、B两点,与y轴交于C点,且对称轴为x=1,点B坐标为(-1,0).则下面的四个结论:
如图,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A、B两点,与y轴交于C点,且对称轴为x=1,点B坐标为(-1,0).则下面的四个结论: 已知:正方形ABCD中,BE=CF,AE、AF的垂线相交于点P,连接EF、CP.求证:CP⊥EF.
已知:正方形ABCD中,BE=CF,AE、AF的垂线相交于点P,连接EF、CP.求证:CP⊥EF.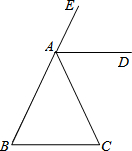 如图,AD是△ABC的外角∠EAC的平分线,且AD∥BC.
如图,AD是△ABC的外角∠EAC的平分线,且AD∥BC.