题目内容
在等腰三角形ABC中，AB=AC，且一腰长与底边的比是5：8，求sinB，cosB的值．
考点：解直角三角形,等腰三角形的性质
专题：
分析：根据等腰三角形的性质可得出AB：AC：BC=5：5：8，再由三角函数的定义可得出sinB，cosB的值．
解答：解：∵AB=AC，∠A=90°，
∴sinB=
=
，cosB=
=
．
∴sinB=
| AC |
| BC |
| 5 |
| 8 |
| AB |
| BC |
| 5 |
| 8 |
点评：本题考查了解直角三角形，等腰三角形的性质，熟记三角函数的定义是解题的关键．
练习册系列答案
阅读快车系列答案
相关题目
若x1，x2是一元二次方程x2-x-1=0的两根，则x1x2的值是（ ）
| A、1 | ||
| B、-1 | ||
C、
| ||
D、-
|
已知：正方形ABCD中，BE=CF，AE、AF的垂线相交于点P，连接EF、CP．求证：CP⊥EF．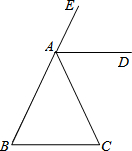
如图，AD是△ABC的外角∠EAC的平分线，且AD∥BC．
已知：线段AB=20cm，如图，点P沿线段AB自A点向B点以2厘米/秒运动，点P出发2秒后，点Q沿线段BA自B点向A点以3厘米/秒运动，问在经过几秒后PQ相距5cm？