题目内容
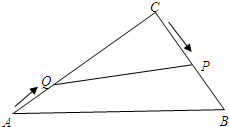 已知:如图,在△ABC中,∠C=Rt∠,AB=10cm,BC=6cm,点P从点C开始沿边CB以2cm/s的速度向点B移动,与此同时,点Q从点A开始沿边AC以1cm/s的速度向点C移动,两点同时出发,当其中一点到达终点时,另一点也随之停止移动.若设移动时间为t秒.
已知:如图,在△ABC中,∠C=Rt∠,AB=10cm,BC=6cm,点P从点C开始沿边CB以2cm/s的速度向点B移动,与此同时,点Q从点A开始沿边AC以1cm/s的速度向点C移动,两点同时出发,当其中一点到达终点时,另一点也随之停止移动.若设移动时间为t秒.(1)当t=1时,求PQ的长;
(2)在整个移动过程中,是否存在某一时刻t,使直线PQ平分△ABC的面积?若存在,请求出t的值;若不存在,请说明理由;
(3)在整个移动过程中,当t=
考点:相似形综合题
专题:
分析:(1)利用勾股定理求得AC的长,在直角△CPQ中利用勾股定理即可求解;
(2)直线PQ平分△ABC的面积,则S△CPQ=
S△ABC,据此即可列方程求得t的值;
(3)根据勾股定理,利用t表示出PQ2的长,然后根据函数的性质即可求解.
(2)直线PQ平分△ABC的面积,则S△CPQ=
| 1 |
| 2 |
(3)根据勾股定理,利用t表示出PQ2的长,然后根据函数的性质即可求解.
解答:解:(1)在Rt△ABC中,AC=
=8,
则当t=1时,CP=2,CQ=AC-AQ=7,
∴PQ=
=
(cm);
(2)假设存在,则
×2t×(8-t)=
×
×6×8,
解得:t1=2,t2=6,
因为0≤t≤3,所以存在,此时t=2.
(3)PQ2=(2t)2+(8-t)2=5t2-16t+64,
则t=-
=
时,PQ2取得最小值,是
=
,则PQ的最小值是
=
.
故答案是:
,
.
| 102-62 |
则当t=1时,CP=2,CQ=AC-AQ=7,
∴PQ=
| 72+22 |
| 53 |
(2)假设存在,则
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解得:t1=2,t2=6,
因为0≤t≤3,所以存在,此时t=2.
(3)PQ2=(2t)2+(8-t)2=5t2-16t+64,
则t=-
| -16 |
| 10 |
| 8 |
| 5 |
| 4×5×64-162 |
| 20 |
| 256 |
| 5 |
|
16
| ||
| 5 |
故答案是:
| 8 |
| 5 |
| 16 |
| 5 |
| 5 |
点评:本题考查了勾股定理以及二次函数的性质,利用二次函数的性质解决实际问题中的最值问题.

练习册系列答案
相关题目
如图,∠1与∠2是对顶角的是( )
A、 |
B、 |
C、 |
D、 |
 已知:正方形ABCD中,BE=CF,AE、AF的垂线相交于点P,连接EF、CP.求证:CP⊥EF.
已知:正方形ABCD中,BE=CF,AE、AF的垂线相交于点P,连接EF、CP.求证:CP⊥EF. 已知:线段AB=20cm,如图,点P沿线段AB自A点向B点以2厘米/秒运动,点P出发2秒后,点Q沿线段BA自B点向A点以3厘米/秒运动,问在经过几秒后PQ相距5cm?
已知:线段AB=20cm,如图,点P沿线段AB自A点向B点以2厘米/秒运动,点P出发2秒后,点Q沿线段BA自B点向A点以3厘米/秒运动,问在经过几秒后PQ相距5cm? 如图,已知D、E分别是△ABC的边AB、AC上的点,G、F是BC上的点,且四边形DGFE是正方形,
如图,已知D、E分别是△ABC的边AB、AC上的点,G、F是BC上的点,且四边形DGFE是正方形,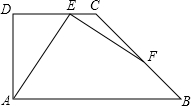 如图,在直角梯形ABCD中,AB∥DC,∠D=90°,AD=CD=4,∠B=45°,点E为直线DC上一点,连接AE,作EF⊥AE交直线CD于点F.
如图,在直角梯形ABCD中,AB∥DC,∠D=90°,AD=CD=4,∠B=45°,点E为直线DC上一点,连接AE,作EF⊥AE交直线CD于点F.