题目内容
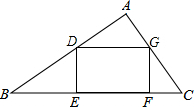 在△ABC中,BC=10,S△ABC=30,矩形DEFG内接于△ABC,设DE=x,S矩形DEFG=y.求:
在△ABC中,BC=10,S△ABC=30,矩形DEFG内接于△ABC,设DE=x,S矩形DEFG=y.求:(1)y与x的函数关系式及定义域;
(2)当x为何值时,四边形DEFG为正方形,求正方形DEFG的面积.
考点:相似三角形的判定与性质,矩形的性质,正方形的性质
专题:
分析:(1)过点A作AH⊥BC于点H,交DG于点K,根据在△ABC中,BC=10,S△ABC=30可得出AG的长,由DE=x,S矩形DEFG=y可知DG=
,再根据DG∥BC可得出△ADG∽△ABC,由此可得出结论;
(2)根据(1)中y与x的关系式得出DG的长,由正方形的边长相等即可得出结论.
| y |
| x |
(2)根据(1)中y与x的关系式得出DG的长,由正方形的边长相等即可得出结论.
解答: 解(1)点A作AH⊥BC于点H,交DG于点K,
解(1)点A作AH⊥BC于点H,交DG于点K,
∵△ABC中BC=10,S△ABC=30,
∴30=
×10×AH,
解得AH=6.
∵DE=x,S矩形DEFG=y,
∴DG=
,
∵DG∥BC,
∴△ADG∽△ABC,
∴
=
,即
=
,
解得AK=
,
∴KH=6-
,
∴x=6-
,整理得y=10x-
x2(0<x<6);
(2)由(1)知y=10x-
x2=x[10-
x],
∵矩形DEFG的边长DE=x,
∴边DE的邻边DG=10-
x
∵当矩形DEFG为正方形时,x=10-
x,
解得x=
,
∴当x=
时,四边形DEFG为正方形,S正方形DEFG=x2=(
)2=
.
 解(1)点A作AH⊥BC于点H,交DG于点K,
解(1)点A作AH⊥BC于点H,交DG于点K,∵△ABC中BC=10,S△ABC=30,
∴30=
| 1 |
| 2 |
解得AH=6.
∵DE=x,S矩形DEFG=y,
∴DG=
| y |
| x |
∵DG∥BC,
∴△ADG∽△ABC,
∴
| AK |
| AH |
| DG |
| BC |
| AK |
| 6 |
| ||
| 10 |
解得AK=
| 3y |
| 5x |
∴KH=6-
| 3y |
| 5x |
∴x=6-
| 3y |
| 5x |
| 5 |
| 3 |
(2)由(1)知y=10x-
| 5 |
| 3 |
| 5 |
| 3 |
∵矩形DEFG的边长DE=x,
∴边DE的邻边DG=10-
| 5 |
| 3 |
∵当矩形DEFG为正方形时,x=10-
| 5 |
| 3 |
解得x=
| 15 |
| 4 |
∴当x=
| 15 |
| 4 |
| 15 |
| 4 |
| 225 |
| 16 |
点评:本题考查的是相似三角形的判定与性质,熟知相似三角形的对应边成比例是解答此题的关键.

练习册系列答案
相关题目
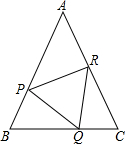 如图,在△ABC中,AB=AC,P、Q、R分别在AB、AC上,且BP=CQ,BQ=CR.
如图,在△ABC中,AB=AC,P、Q、R分别在AB、AC上,且BP=CQ,BQ=CR. 已知:正方形ABCD中,BE=CF,AE、AF的垂线相交于点P,连接EF、CP.求证:CP⊥EF.
已知:正方形ABCD中,BE=CF,AE、AF的垂线相交于点P,连接EF、CP.求证:CP⊥EF.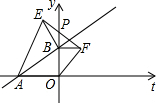 如图,平面直角坐标系中点A的坐标为(-4,0),点B的坐标为(0,m)(其中m>0).
如图,平面直角坐标系中点A的坐标为(-4,0),点B的坐标为(0,m)(其中m>0). (用反证法证明)已知直线a∥c,b∥c,求证:a∥b.
(用反证法证明)已知直线a∥c,b∥c,求证:a∥b.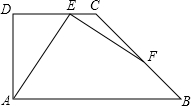 如图,在直角梯形ABCD中,AB∥DC,∠D=90°,AD=CD=4,∠B=45°,点E为直线DC上一点,连接AE,作EF⊥AE交直线CD于点F.
如图,在直角梯形ABCD中,AB∥DC,∠D=90°,AD=CD=4,∠B=45°,点E为直线DC上一点,连接AE,作EF⊥AE交直线CD于点F.