题目内容
已知关于x的方程k2x2﹣2(k+1)x+1=0有两个实数根.
(1)求k的取值范围;
(2)当k=1时,设所给方程的两个根分别为x1和x2,求(x1﹣2)(x2﹣2)的值.
(1)k≥﹣且k≠0;(2)﹣3. 【解析】试题分析:(1)根据根的判别式得出k的取值范围即可; (2)把k=1代入即可得出方程,根据根与系数的关系得出x1+x2,x1x2,再代入计算即可. 试题解析: (1)根据题意得k2≠0且△=4(k+1)2﹣4k2≥0, 解得k≥﹣且k≠0; (2)k=1时方程化为x2﹣4x+1=0,则x1+x2=4,x1•x2=1, ...
练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目


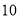 元和
元和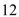 元的两种书共
元的两种书共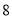 本,其中单价为
本,其中单价为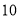 元的书
元的书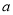 本,则一共应付_______元.
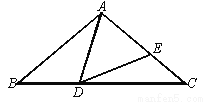
本,则一共应付_______元.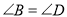 ,添加下列条件,不能得到△ABC与△ADE相似的是( )
,添加下列条件,不能得到△ABC与△ADE相似的是( )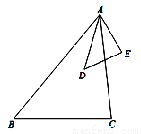
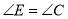 B.
B. 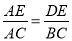 C.
C. 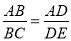 D.
D.