题目内容
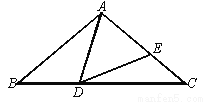
如图,在△ABC中,AB = AC = 2,∠B =∠C = 50°,点D在线段BC上运动(点D不与B、C重合),连结AD,作∠ADE = 50°,DE交线段AC于点E.
(1)若DC = 2,求证:△ABD≌△DCE;
(2)在点D的运动过程中,△ADE的形状可以是等腰三角形吗?若可以,请求出∠BDA的度数;若不可以,请说明理由.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
题目内容
如图,在△ABC中,AB = AC = 2,∠B =∠C = 50°,点D在线段BC上运动(点D不与B、C重合),连结AD,作∠ADE = 50°,DE交线段AC于点E.
(1)若DC = 2,求证:△ABD≌△DCE;
(2)在点D的运动过程中,△ADE的形状可以是等腰三角形吗?若可以,请求出∠BDA的度数;若不可以,请说明理由.

 阅读快车系列答案
阅读快车系列答案