��Ŀ����
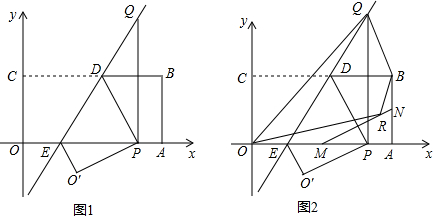
2����ͼ1��������OABC����ƽ��ֱ������ϵxOy�У���A��C�ֱ���x��y��������ᣬ��B��4��2����������OABC���ۣ�ʹ�õ�C�����߶�OA�ϣ����ۺ��C�Ķ�Ӧ��ΪP���ۺ�����ֱ�߷ֱ�ֱ��BC��ֱ��OA�ڵ�D��E����P��OA�Ĵ��߽��ۺ�����ֱ���ڵ�Q������P���߶�OA�������˵�O��A�����˶�ʱ�����Q������Ϊ��x��y������1����y����x�ĺ�������ʽ���Ա���x��ȡֵ��Χ��
��2����ͼ2��M��N�ֱ��DZ�OA��AB���е㣬R���߶�MN�ϵĶ��㣬���ı���ORBQ�����ΪS����xΪ��ֵʱ��Sȡ����Сֵ�����������Сֵ��
���� ��1������CQ��PQ��BD�ڵ�F�����۵������ʵó�CQ=PQ���ɹ��ɶ����ó�x2+��y-2��2=y2�����ɵó������
��2������OB��MB������������λ�߶����ó�MN��OB�����S��OBR=S��OBM=$\frac{1}{2}$OM��AB=2����ֱ��OB��ֱ��PQ�ཻ�ڵ�G��x��$\frac{x}{2}$�������S��OBQ=S��OGQ+S��BGQ=$\frac{1}{2}$x2-x+2���ó�S��x�Ķ��κ��������ɵó������
��� �⣺ ��1������CQ��PQ��BD�ڵ�F����ͼ1��ʾ��
��1������CQ��PQ��BD�ڵ�F����ͼ1��ʾ��
���۵������ʵã�CQ=PQ��
��B��4��2����Q��x��y����
����Rt��CFQ��CF=x��QF=y-2��CQ=y��
��x2+��y-2��2=y2��
��y=$\frac{1}{4}$x2+1��
�ߵ���P���߶�OA�������˵�O��A�����˶���
���Ա���x��ȡֵ��ΧΪ��0��x��4��
��2������OB��MB����ͼ2��ʾ��
��M��N�ֱ��DZ�OA��AB���е㣬
��MN��OB��
��S��OBR=S��OBM=$\frac{1}{2}$OM��AB=$\frac{1}{2}$��2��2=2��
��ֱ��OB��ֱ��PQ�ཻ�ڵ�G��x��$\frac{x}{2}$����
��S��OBQ=S��OGQ+S��BGQ=$\frac{1}{2}$QG•OA=$\frac{1}{2}$��y-$\frac{x}{2}$����4=2��$\frac{1}{4}$x2+1-$\frac{x}{2}$��=$\frac{1}{2}$x2-x+2��
��S=S��OBR+S��OBQ=$\frac{1}{2}$x2-x+2+2=$\frac{1}{2}$x2-x+4=$\frac{1}{2}$��x-1��2+$\frac{7}{2}$��0��x��4����
�൱x=1ʱ��S����Сֵ=$\frac{7}{2}$��
���� �����Ǽ��α任�ۺ���Ŀ�������˾��ε����ʡ����۱任�����ʡ����ɶ�������������λ�߶���������������ļ��㡢���κ�������ֵ��֪ʶ�������ۺ���ǿ����һ���Ѷȣ����S��x�Ķ��κ����ǽ�����⣨2���Ĺؼ���

 ����νӽ̲���ĩ���Ԥϰ�人������ϵ�д�
����νӽ̲���ĩ���Ԥϰ�人������ϵ�д� ������ҵ��ٳɳ����½������������ϵ�д�
������ҵ��ٳɳ����½������������ϵ�д�| A�� | -5 | B�� | 5 | C�� | -20 | D�� | 20 |
| A�� | 0.1126��1010 | B�� | 1.126��109 | C�� | 1.126��108 | D�� | 11.26��107 |
| A�� | $\frac{a+b}{a}$ | B�� | $\frac{b}{a+b}$ | C�� | $\frac{b-a}{a+b}$ | D�� | $\frac{a+b}{b-a}$ |