题目内容
1．解不等式组：$\left\{\begin{array}{l}{x+1≥1}\\{3x-1＜2（x+1）}\end{array}\right.$．分析 分别求出各不等式的解集，再求出其公共解集即可．
解答 解：$\left\{\begin{array}{l}x+1≥1①\\ 3x-1＜2（x+1）②\end{array}\right.$，由①得，x≥0，由②得，x＜3，
所以原不等式组的解为：0≤x＜3．
点评 本题考查的是解一元一次不等式组，熟知“同大取大；同小取小；大小小大中间找；大大小小找不到”的原则是解答此题的关键．
练习册系列答案
名校课堂系列答案
相关题目
11．上网流量、语音通话是手机通信消费的两大主体，目前，某通信公司推出消费优惠新招--“定制套餐”，消费者可根据实际情况自由定制每月上网流量与语音通话时间，并按照二者的阶梯资费标准缴纳通信费．下表是流量与语音的阶梯定价标准．
【小提示：阶梯定价收费计算方法，如600分钟语音通话费=0.15×500+0.12×（600-500）=87元】
（1）甲定制了600MB的月流量，花费48元；乙定制了2GB的月流量，花费120.4元，求a，b的值．（注：1GB=1024MB）
（2）甲的套餐费用为199元，其中含600MB的月流量；丙的套餐费用为244.2元，其中包含1GB的月流量，二人均定制了超过1000分钟的每月通话时间，并且丙的语音通话时间比甲多300分钟，求m的值．
| 流量阶梯定价标准 | |
| 使用范围 | 阶梯单价（元/MB） |
| 1-100MB | a |
| 101-500MB | 0.07 |
| 501MB-20GB | b |
| 语音阶梯定价标准 | |
| 使用范围 | 阶梯资费（元/分钟） |
| 1-500分钟 | 0.15 |
| 501-1000分钟 | 0.12 |
| 1001-2000分钟 | m |
（1）甲定制了600MB的月流量，花费48元；乙定制了2GB的月流量，花费120.4元，求a，b的值．（注：1GB=1024MB）
（2）甲的套餐费用为199元，其中含600MB的月流量；丙的套餐费用为244.2元，其中包含1GB的月流量，二人均定制了超过1000分钟的每月通话时间，并且丙的语音通话时间比甲多300分钟，求m的值．
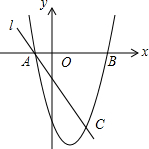如图，抛物线y=x2-2x-3与x轴交于A、B两点（A点在B点左侧），直线l与抛物线交于A、C两点，其中C点的横坐标为2．
9．下列运算正确的是（ ）
| A． | 4a-a=3 | B． | a6÷a3=a3 | C． | （ab）2=ab2 | D． | （a-b）2=a2-b2 |
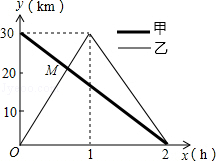在一条笔直的公路上有A、B两地，甲骑自行车从A地到B地；乙骑自行车从B地到A地，到达A地后立即按原路返回，如图是甲、乙两人离B地的距离y（km）与行驶时间x（h）之间的函数图象，根据图象解答以下问题：
6．计算-1+2的结果是（ ）
| A． | -3 | B． | 3 | C． | 1 | D． | -1 |
