题目内容
12.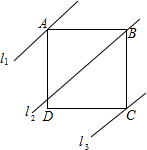 如图,四边形ABCD是正方形,直线l1、l2、l3分别通过A、B、C三点,且l1∥l2∥l3,若l1与l2的距离为6,l2与l3的距离为8,则正方形ABCD的面积等于100.
如图,四边形ABCD是正方形,直线l1、l2、l3分别通过A、B、C三点,且l1∥l2∥l3,若l1与l2的距离为6,l2与l3的距离为8,则正方形ABCD的面积等于100.
分析 画出L1到L2,L2到L3的距离,分别交L2,L3于E,F,通过证明△ABE≌△BCF,得出BF=AE,再由勾股定理即可得出结论.
解答 解:过点A作AE⊥l1,过点C作CF⊥l2,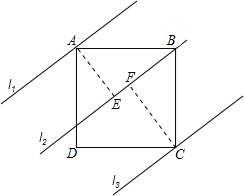
∴∠CBF+∠BCF=90°,
四边形ABCD是正方形,
∴AB=BC=CD=AD,
∴∠DAB=∠ABC=∠BCD=∠CDA=90°,
∴∠ABE+∠CBF=90°,
∵l1∥l2∥l3,
∴∠ABE=∠BCF,
在△ABE和△BCF中,
$\left\{\begin{array}{l}{∠AEB=∠BFC}\\{∠ABE=∠BCF}\\{AB=BC}\end{array}\right.$,
∴△ABE≌△BCF(AAS),
∴BF=AE,
∴BF2+CF2=BC2,
∴BC2=62+82=100.
即正方形ABCD的面积为100,
故答案为:100.
点评 本题主要考查了正方形的性质,全等三角形的判定与性质以及正方形面积的求解方法,能正确作出辅助线是解此题的关键,难度适中.

练习册系列答案
相关题目
7.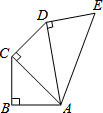 如图所示,AB=BC=CD=DE=1,AB⊥BC,AC⊥CD,AD⊥DE,则五边形ABCDE的面积等于( )
如图所示,AB=BC=CD=DE=1,AB⊥BC,AC⊥CD,AD⊥DE,则五边形ABCDE的面积等于( )
 如图所示,AB=BC=CD=DE=1,AB⊥BC,AC⊥CD,AD⊥DE,则五边形ABCDE的面积等于( )
如图所示,AB=BC=CD=DE=1,AB⊥BC,AC⊥CD,AD⊥DE,则五边形ABCDE的面积等于( )| A. | $\frac{3}{2}$ | B. | $\frac{3}{2}$$\sqrt{2}$ | C. | $\frac{3}{2}$$\sqrt{3}$ | D. | $\frac{1+\sqrt{2}+\sqrt{3}}{2}$ |
4.在代数式$\frac{a}{3}$、$\frac{x}{x+1}$、$\frac{1}{5}$x+y、$\frac{{a}^{2}-{b}^{2}}{a-b}$,$\frac{3}{π}$中分式有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
2.一个凸n边形,其每个内角都是140°,则n的值为( )
| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
 如图,从地面上的点A看一山坡上的电线杆PQ,测得杆顶端点P的仰角是45°,向前走6m到达B点,测得杆顶端点P和杆底端点Q的仰角分别是60°和30°.
如图,从地面上的点A看一山坡上的电线杆PQ,测得杆顶端点P的仰角是45°,向前走6m到达B点,测得杆顶端点P和杆底端点Q的仰角分别是60°和30°.