题目内容
2.一个凸n边形,其每个内角都是140°,则n的值为( )| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
分析 根据多边形每个内角与其相邻的内角互补,则正n边形的每个外角的度数=180°-140°=40°,然后根据多边形的外角和为360°即可得到n的值.
解答 解:∵正n边形的每个内角都是140°,
∴正n边形的每个外角的度数=180°-140°=40°,
∴n=$\frac{360}{40}$=9.
故选D.
点评 本题考查了多边形的外角和定理:多边形的外角和为360°.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
13.化简$\sqrt{16}$的结果是( )
| A. | ±4 | B. | 4 | C. | 2 | D. | ±2 |
10.下列各组数据中,能构成三角形的是( )
| A. | 1cm、2cm、3cm | B. | 2cm、3cm、4cm | C. | 4cm、9cm、4cm | D. | 2cm、1cm、4cm |
12. 如图,PA和PB是⊙O的切线,点A和点B是切点,AC是⊙O的直径,已知∠P=40°,则∠ACB的大小是( )
如图,PA和PB是⊙O的切线,点A和点B是切点,AC是⊙O的直径,已知∠P=40°,则∠ACB的大小是( )
 如图,PA和PB是⊙O的切线,点A和点B是切点,AC是⊙O的直径,已知∠P=40°,则∠ACB的大小是( )
如图,PA和PB是⊙O的切线,点A和点B是切点,AC是⊙O的直径,已知∠P=40°,则∠ACB的大小是( )| A. | 40° | B. | 60° | C. | 70° | D. | 80° |
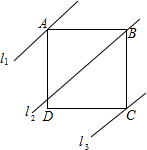 如图,四边形ABCD是正方形,直线l1、l2、l3分别通过A、B、C三点,且l1∥l2∥l3,若l1与l2的距离为6,l2与l3的距离为8,则正方形ABCD的面积等于100.
如图,四边形ABCD是正方形,直线l1、l2、l3分别通过A、B、C三点,且l1∥l2∥l3,若l1与l2的距离为6,l2与l3的距离为8,则正方形ABCD的面积等于100. 已知某商品每件的成本为20元,第x天(x≤90)的售价和销量分别为y元/件和(180-2x)件,设第x天该商品的销售利润为w元,请根据所给图象解决下列问题:
已知某商品每件的成本为20元,第x天(x≤90)的售价和销量分别为y元/件和(180-2x)件,设第x天该商品的销售利润为w元,请根据所给图象解决下列问题: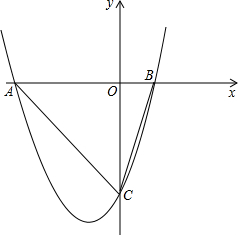 已知抛物线y=x2+2x-3与x轴交于A,B(点A在点B的左侧)两单,与y轴交于点C.
已知抛物线y=x2+2x-3与x轴交于A,B(点A在点B的左侧)两单,与y轴交于点C.