题目内容
17.先化简,再求值:($\frac{{a}^{2}}{a-1}$+$\frac{1}{1-a}$)•$\frac{1}{a}$,其中a=-$\frac{1}{2}$.分析 原式括号中第二项变形后,利用同分母分式的减法法则计算,约分得到最简结果,把a的值代入计算即可求出值.
解答 解:原式=($\frac{{a}^{2}}{a-1}$-$\frac{1}{a-1}$)•$\frac{1}{a}$=$\frac{(a+1)(a-1)}{a-1}$•$\frac{1}{a}$=$\frac{a+1}{a}$,
当a=-$\frac{1}{2}$时,原式=-1.
点评 此题考查了分式的化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案
相关题目
12.下列几何体中,俯视图是矩形的是( )
| A. |  | B. |  | C. |  | D. |  |
2.下列计算正确的是( )
| A. | x2+x3=x5 | B. | (x3)3=x6 | C. | x•x2=x2 | D. | x(2x)2=4x3 |
9.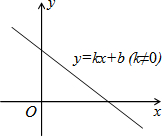 一次函数y=kx+b(k≠0)在平面直角坐标系内的图象如图所示,则k和b的取值范围是( )
一次函数y=kx+b(k≠0)在平面直角坐标系内的图象如图所示,则k和b的取值范围是( )
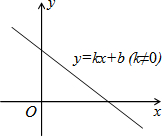 一次函数y=kx+b(k≠0)在平面直角坐标系内的图象如图所示,则k和b的取值范围是( )
一次函数y=kx+b(k≠0)在平面直角坐标系内的图象如图所示,则k和b的取值范围是( )| A. | k>0,b>0 | B. | k<0,b<0 | C. | k<0,b>0 | D. | k>0,b<0 |
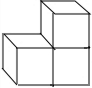 用3个完全相同的小正方体组成如图所示的几何体,则它的俯视图是( )
用3个完全相同的小正方体组成如图所示的几何体,则它的俯视图是( )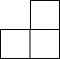


 如图,在正方形ABCD中,G是BC上任意一点,连接AG,DE⊥AG于E,BF∥DE交AG于F,探究线段AF、BF、EF三者之间的数量关系,并说明理由.
如图,在正方形ABCD中,G是BC上任意一点,连接AG,DE⊥AG于E,BF∥DE交AG于F,探究线段AF、BF、EF三者之间的数量关系,并说明理由.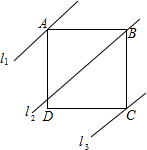 如图,四边形ABCD是正方形,直线l1、l2、l3分别通过A、B、C三点,且l1∥l2∥l3,若l1与l2的距离为6,l2与l3的距离为8,则正方形ABCD的面积等于100.
如图,四边形ABCD是正方形,直线l1、l2、l3分别通过A、B、C三点,且l1∥l2∥l3,若l1与l2的距离为6,l2与l3的距离为8,则正方形ABCD的面积等于100.