题目内容
1.已知x+y=3,xy=2,求x2+y2,x-y的值.分析 根据完全平方公式的变形来a2+b2=(a+b)2-2ab和(a-b)2=(a+b)2-4ab求解.
解答 解:∵x+y=3,xy=2,
∴x2+y2=(x+y)2-2xy=32-2×2=5,即x2+y2=5.
(x-y)2=(x+y)2-4xy=32-4×2=1,
则x-y=±1.
点评 本题主要考查完全平方公式,熟记公式的几个变形公式对解题大有帮助.

练习册系列答案
相关题目
9.下列各组数中,不能作为直角三角形的三边长的是( )
| A. | 0.3,0.4,0.5 | B. | 8,9,10 | C. | 7,24,25 | D. | 9,12,15 |
16.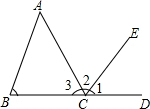 如图,下列说法正确的是( )
如图,下列说法正确的是( )
 如图,下列说法正确的是( )
如图,下列说法正确的是( )| A. | ∠2和∠B是同位角 | B. | ∠2和∠B是内错角 | ||
| C. | ∠1和∠A是内错角 | D. | ∠3和∠B是同旁内角 |
13.化简$\sqrt{16}$的结果是( )
| A. | ±4 | B. | 4 | C. | 2 | D. | ±2 |
10.下列各组数据中,能构成三角形的是( )
| A. | 1cm、2cm、3cm | B. | 2cm、3cm、4cm | C. | 4cm、9cm、4cm | D. | 2cm、1cm、4cm |
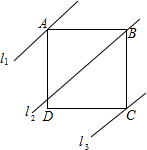 如图,四边形ABCD是正方形,直线l1、l2、l3分别通过A、B、C三点,且l1∥l2∥l3,若l1与l2的距离为6,l2与l3的距离为8,则正方形ABCD的面积等于100.
如图,四边形ABCD是正方形,直线l1、l2、l3分别通过A、B、C三点,且l1∥l2∥l3,若l1与l2的距离为6,l2与l3的距离为8,则正方形ABCD的面积等于100.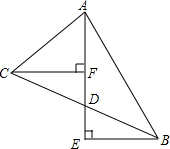 如图,BE⊥AE于E,CF⊥AE于F,D是EF的中点,求证:CD=BD.
如图,BE⊥AE于E,CF⊥AE于F,D是EF的中点,求证:CD=BD.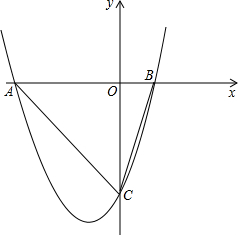 已知抛物线y=x2+2x-3与x轴交于A,B(点A在点B的左侧)两单,与y轴交于点C.
已知抛物线y=x2+2x-3与x轴交于A,B(点A在点B的左侧)两单,与y轴交于点C.