题目内容
17.已知y<$\sqrt{x-2}$+$\sqrt{2-x}$+3,化简|y-3|-$\sqrt{{y}^{2}-8y+16}$.分析 根据二次根式的性质被开方数大于或等于0,即可求得x的值,然后求得y的范围,根据绝对值以及二次根式的性质进行化简.
解答 解:根据题意得:$\left\{\begin{array}{l}{x-2≥0}\\{2-x≥0}\end{array}\right.$,解得:x=2,
则y<3,
则原式=3-y-|y-4|=3-y-(4-y)=-2y-1.
点评 本题主要考查了二次根式的意义和性质.概念:式子$\sqrt{a}$(a≥0)叫二次根式.性质:二次根式中的被开方数必须是非负数,否则二次根式无意义.求得x的值是关键.

练习册系列答案
相关题目
2.下列计算正确的是( )
| A. | x2+x3=x5 | B. | (x3)3=x6 | C. | x•x2=x2 | D. | x(2x)2=4x3 |
9.下列各组数中,不能作为直角三角形的三边长的是( )
| A. | 0.3,0.4,0.5 | B. | 8,9,10 | C. | 7,24,25 | D. | 9,12,15 |
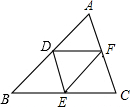 如图所示,在△ABC中,D,E,F分别是AB,BC,AC上的点,且DE∥AC,EF∥AB,DF∥BC,则图中平行四边形共有( )
如图所示,在△ABC中,D,E,F分别是AB,BC,AC上的点,且DE∥AC,EF∥AB,DF∥BC,则图中平行四边形共有( )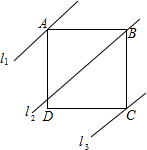 如图,四边形ABCD是正方形,直线l1、l2、l3分别通过A、B、C三点,且l1∥l2∥l3,若l1与l2的距离为6,l2与l3的距离为8,则正方形ABCD的面积等于100.
如图,四边形ABCD是正方形,直线l1、l2、l3分别通过A、B、C三点,且l1∥l2∥l3,若l1与l2的距离为6,l2与l3的距离为8,则正方形ABCD的面积等于100.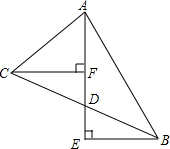 如图,BE⊥AE于E,CF⊥AE于F,D是EF的中点,求证:CD=BD.
如图,BE⊥AE于E,CF⊥AE于F,D是EF的中点,求证:CD=BD.