题目内容
12.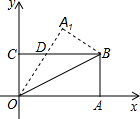 如图,在平面直角坐标系中,将矩形OABC沿对角线OB对折,使点A($\sqrt{3}$,0)落在点A1处,已知点B的坐标是($\sqrt{3}$,1),则点A1的坐标是( )
如图,在平面直角坐标系中,将矩形OABC沿对角线OB对折,使点A($\sqrt{3}$,0)落在点A1处,已知点B的坐标是($\sqrt{3}$,1),则点A1的坐标是( )| A. | ($\frac{1}{2}$,$\frac{{\sqrt{3}}}{2}$) | B. | ($\frac{{\sqrt{3}}}{2}$,$\frac{3}{2}$) | C. | ($\frac{{\sqrt{3}}}{2}$,2) | D. | ($\frac{3}{2}$,$\frac{{\sqrt{3}}}{2}$) |
分析 由已知可得∠AOB=30°,翻折后找到相等的角及相等的边,在直角三角形中,利用勾股定理可求得答案.
解答 解:过A1作A1D⊥OA,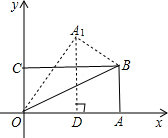
∵A($\sqrt{3}$,0),B的坐标是($\sqrt{3}$,1),
∴OA=$\sqrt{3}$,AB=1,
在Rt△OAB中,OB=$\sqrt{(\sqrt{3})^{2}+{1}^{2}}$=2,AB=1,
∴AB=$\frac{1}{2}$OB,
∵△AOB是直角三角形,
∴∠AOB=30°,
OB为折痕,
∴∠A1OB=∠AOB=30°,OA1=OA=$\sqrt{3}$,
Rt△OA1D中,∠OA1D=30°,
∴OD=$\frac{1}{2}$×$\sqrt{3}$=$\frac{\sqrt{3}}{2}$,
A1D=$\frac{\sqrt{3}}{2}$×$\sqrt{3}$=$\frac{3}{2}$,
∴点A1的坐标($\frac{\sqrt{3}}{2}$,$\frac{3}{2}$).
故选B.
点评 本题考查了含30°的直角三角形的性质、勾股定理及翻折问题;利用翻折找准相等的角、相等的边是正确解答本题的关键.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
2.已知小明上学时,走上坡路,速度为m千米/时;放学回家时,沿原路返回,速度为n千米/时,则小明上学和放学时的平均速度为( )
| A. | $\frac{m+n}{2}$千米/时 | B. | $\frac{mn}{m+n}$千米/时 | C. | $\frac{2mn}{m+n}$千米/时 | D. | $\frac{m+n}{mn}$千米/时 |
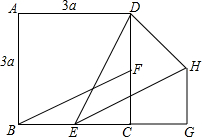 如图,正方形ABCD的边长为3a,两动点E、F分别从顶点B、C同时开始以相同速度沿BC、CD运动,与△BCF相应的△EGH在运动过程中始终保持△EGH≌△BCF,B、E、C、G在一直线上,△DHE的面积的最小值是$\frac{27}{8}$a2.
如图,正方形ABCD的边长为3a,两动点E、F分别从顶点B、C同时开始以相同速度沿BC、CD运动,与△BCF相应的△EGH在运动过程中始终保持△EGH≌△BCF,B、E、C、G在一直线上,△DHE的面积的最小值是$\frac{27}{8}$a2.