题目内容
11.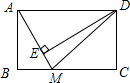 如图,矩形ABCD中,AB=4,AD=9,点M在BC上,且BM:MC=1:2,DE⊥AM于点E,求DE的长为$\frac{36}{5}$.
如图,矩形ABCD中,AB=4,AD=9,点M在BC上,且BM:MC=1:2,DE⊥AM于点E,求DE的长为$\frac{36}{5}$.
分析 根据比例求出BM,再利用勾股定理列式求出AM,然后求出△ABM和△DEA,再根据相似三角形对应边成比例列式计算即可得解.
解答 解:∵四边形ABCD是矩形,
∴BC=AD=9,∠B=90°,
∵BM:MC=1:2,
∴BM=$\frac{1}{3}$×9=3,
在Rt△ABM中,AM=$\sqrt{A{B}^{2}+B{M}^{2}}$=$\sqrt{{4}^{2}+{3}^{2}}$=5,
∵DE⊥AM,
∴∠AED=90°,
∴∠DAE+∠ADE=90°,
∵∠BAM+∠DAE=90°,
∴∠BAM=∠ADE,
又∵∠B=∠AED=90°,
∴△ABM∽△DEA,
∴$\frac{DE}{AB}=\frac{AD}{AM}$,即$\frac{DE}{4}=\frac{9}{5}$,
∴DE=$\frac{36}{5}$;
故答案为:$\frac{36}{5}$.
点评 本题考查了矩形的性质,勾股定理,相似三角形的判定与性质;证明相似三角形得出比例式是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
2.已知小明上学时,走上坡路,速度为m千米/时;放学回家时,沿原路返回,速度为n千米/时,则小明上学和放学时的平均速度为( )
| A. | $\frac{m+n}{2}$千米/时 | B. | $\frac{mn}{m+n}$千米/时 | C. | $\frac{2mn}{m+n}$千米/时 | D. | $\frac{m+n}{mn}$千米/时 |
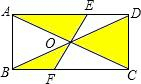 如图,矩形ABCD中,对角线AC、BD交于点O,过O的直线分别交AD、BC于点E、F,已知AD=4cm,图中阴影部分的面积总和为6cm2,对角线AC长为( )
如图,矩形ABCD中,对角线AC、BD交于点O,过O的直线分别交AD、BC于点E、F,已知AD=4cm,图中阴影部分的面积总和为6cm2,对角线AC长为( )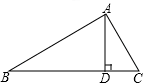 如图,已知Rt△ABC中,斜边BC上的高AD=4,cosB=$\frac{4}{5}$.求AC边的长度.
如图,已知Rt△ABC中,斜边BC上的高AD=4,cosB=$\frac{4}{5}$.求AC边的长度.
 如图,以正方形ABCD的对角线BD为边作等边三角形BDE,过E作EF⊥AD,交DA的延长线于F,则∠AEF的度数为45°;若等边三角形BDE的面积为18$\sqrt{2}$cm2,则正方形的面积为12$\sqrt{6}$cm2.
如图,以正方形ABCD的对角线BD为边作等边三角形BDE,过E作EF⊥AD,交DA的延长线于F,则∠AEF的度数为45°;若等边三角形BDE的面积为18$\sqrt{2}$cm2,则正方形的面积为12$\sqrt{6}$cm2.