题目内容
14. 如图,在?ABCD中,DE⊥AB于点E,DF⊥BC于点F,且∠ADE+∠CDF=60°,求∠EDF的度数60°.
如图,在?ABCD中,DE⊥AB于点E,DF⊥BC于点F,且∠ADE+∠CDF=60°,求∠EDF的度数60°.
分析 首先根据平行四边形的性质可得∠A=∠C,DC∥AB,进而可得∠A+∠ADC=180°,再由DE⊥AB,DF⊥BC可证出∠CDF=∠ADE,根据∠ADE+∠CDF=60°可得∠CDF=∠ADE=30°,进而可得∠EDF的度数.
解答 解:∵四边形ABCD是平行四边形,
∴∠A=∠C,DC∥AB,
∴∠A+∠ADC=180°,
∵DF⊥BC,DE⊥AB,
∴∠DFC=90°,∠C+∠CDF=90°,
∴∠CDF=∠ADE,
∵∠ADE+∠CDF=60°,
∴∠ADE=∠CDF=30°,
∴∠A=60°,
∴∠ADC=120°,
∴∠EDF=60°.
故答案为:60°.
点评 此题主要考查了平行四边形的性质,掌握平行四边形对角相等,对边平行,解决此题的关键是证明∠CDF=∠ADE.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.已知小明上学时,走上坡路,速度为m千米/时;放学回家时,沿原路返回,速度为n千米/时,则小明上学和放学时的平均速度为( )
| A. | $\frac{m+n}{2}$千米/时 | B. | $\frac{mn}{m+n}$千米/时 | C. | $\frac{2mn}{m+n}$千米/时 | D. | $\frac{m+n}{mn}$千米/时 |
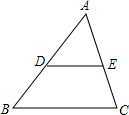 如图,在△ABC中,D、E分别为AB、AC的中点,连接DE,若S△ADE=2,则四边形BDEC的面积为6.
如图,在△ABC中,D、E分别为AB、AC的中点,连接DE,若S△ADE=2,则四边形BDEC的面积为6.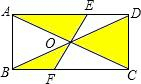 如图,矩形ABCD中,对角线AC、BD交于点O,过O的直线分别交AD、BC于点E、F,已知AD=4cm,图中阴影部分的面积总和为6cm2,对角线AC长为( )
如图,矩形ABCD中,对角线AC、BD交于点O,过O的直线分别交AD、BC于点E、F,已知AD=4cm,图中阴影部分的面积总和为6cm2,对角线AC长为( )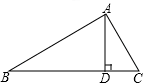 如图,已知Rt△ABC中,斜边BC上的高AD=4,cosB=$\frac{4}{5}$.求AC边的长度.
如图,已知Rt△ABC中,斜边BC上的高AD=4,cosB=$\frac{4}{5}$.求AC边的长度.