题目内容
 (1)计算:
(1)计算:| 12 |
| 1 |
| 2 |
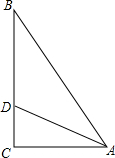
(2)已知,如图△ABC中,∠C=90°,AD平分∠BAC,CD=
| 3 |
| 3 |
考点:角平分线的性质,实数的运算,负整数指数幂,勾股定理,特殊角的三角函数值
专题:
分析:(1)首先根据二次根式的化简、负整数指数幂、特殊角的三角函数计算,然后再计算加减即可;
(2)过D作DE⊥AB,首先根据角平分线的性质可得DE=CD=
,然后再计算出∠B的度数,然后利用三角函数计算出AB,AC的长.
(2)过D作DE⊥AB,首先根据角平分线的性质可得DE=CD=
| 3 |
解答: 解:(1)原式=2
解:(1)原式=2
-8-6×
-1=2
-8-3
-1=-9-
;
(2)过D作DE⊥AB,
∵AD平分∠BAC,
∴DE=CD=
,
∵DB=2
,
∴sinB=
=
,
∴∠B=30°,
∴AB=
=6,
AC=CB×tan30°=3,
∵∠B=30°,
∴∠BAC=60°,
∵AD平分∠BAC,
∴∠DAC=30°,
∵CD=
,
∴AD=2
.
 解:(1)原式=2
解:(1)原式=2| 3 |
| ||
| 2 |
| 3 |
| 3 |
| 3 |
(2)过D作DE⊥AB,
∵AD平分∠BAC,
∴DE=CD=
| 3 |
∵DB=2
| 3 |
∴sinB=
| DE |
| DB |
| 1 |
| 2 |
∴∠B=30°,
∴AB=
| CB |
| cos30° |
AC=CB×tan30°=3,
∵∠B=30°,
∴∠BAC=60°,
∵AD平分∠BAC,
∴∠DAC=30°,
∵CD=
| 3 |
∴AD=2
| 3 |
点评:此题主要考查了实数的运算,以及三角函数的应用和角平分线的性质,关键是掌握特殊角的三角函数值.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
下面各式正确的是( )
A、
| ||
B、±
| ||
C、-
| ||
D、-
|
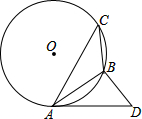 已知AB为⊙O的弦,C为⊙O上一点,∠C=∠BAD,且BD⊥AB于点B,
已知AB为⊙O的弦,C为⊙O上一点,∠C=∠BAD,且BD⊥AB于点B,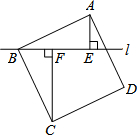 如图,过正方形ABCD的顶点B作直线l,过A、C作l的垂线,垂足分别为E、F.若AE=5,CF=12,则AB的长为
如图,过正方形ABCD的顶点B作直线l,过A、C作l的垂线,垂足分别为E、F.若AE=5,CF=12,则AB的长为
 小明在用图象法解二元一次方程组时所画图象如图,那么这个方程组的解是
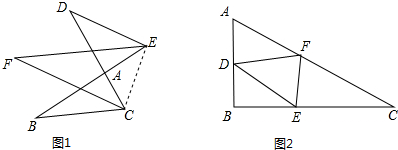
小明在用图象法解二元一次方程组时所画图象如图,那么这个方程组的解是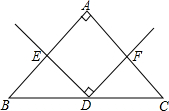 已知:∠A=90°,AB=AC,D是BC的中点,∠EDF=90°.求证:DE=DF.
已知:∠A=90°,AB=AC,D是BC的中点,∠EDF=90°.求证:DE=DF.