Question

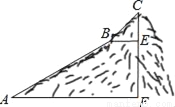
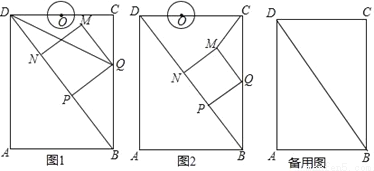
如图，在矩形ABCD中，AB=6cm，AD=8cm，点P从点B出发，沿对角线BD向点D匀速运动，速度为4cm/s，过点P作PQ⊥BD交BC于点Q，以PQ为一边作正方形PQMN，使得点N落在射线PD上．点O从点D出发，沿DC向点C匀速运动，速度为3cm/s，以O为圆心，1cm半径作⊙O．点P与点D同时出发，设它们的运动时间为t（单位：s） （0≤t≤）．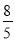

（1）如图1，连接DQ，若DQ平分∠BDC，则t的值为　 　s；

（2）如图2，连接CM，设△CMQ的面积为S，求S关于t的函数关系式；

（3）在运动过程中，当t为何值时，⊙O与MN第一次相切？

（1）1s; （2）S=﹣t2+t；（3）. 【解析】试题分析：（1）由△DQC≌△DQP，推出DP=DC=6，在Rt△ADB中，BD=10，推出PB=4即可解决问题； （2）过点M作MH⊥BC于点H，证明△HMQ∽△PQB，，由=，得MH=t，即可求得△CMQ的面积； （3）设⊙O与MN相切于点E，连接OE，作OF⊥BD于点F，可证得△DFO∽△DCB， 由此即可解得：t...

Answer 1