如图.为测量一座山峰CF的高度.将此山的某侧山坡划分为AB和BC两段.每一段山坡近似是“直的.测得坡长AB=800米.BC=200米.坡角∠BAF=30°.∠CBE=45°．(1)求AB段山坡的高度EF,(2)求山峰的高度CF．米 [解析](1)作BH⊥AF于H.如图.在Rt△ABF中根据正弦的定义可计算出BH的长.从而得到EF的长, (2)先在Rt△CB 题目和参考答案——青夏教育精英家教网——

题目内容

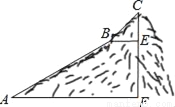
如图，为测量一座山峰CF的高度，将此山的某侧山坡划分为AB和BC两段，每一段山坡近似是“直”的，测得坡长AB=800米，BC=200米，坡角∠BAF=30°，∠CBE=45°．

（1）求AB段山坡的高度EF；

（2）求山峰的高度CF（结果保留根式）．

(1) 400米；(2) （100+400）米【解析】（1）作BH⊥AF于H，如图，在Rt△ABF中根据正弦的定义可计算出BH的长，从而得到EF的长；（2）先在Rt△CBE中利用∠CBE的正弦计算出CE，然后计算CE和EF的和即可．试题解析：（1）作BH⊥AF于H，如图，在Rt△ABH中，∵sin∠BAH=， ∴BH=800•sin30°=400， ∴E...

练习册系列答案

诚成教育学业评价系列答案

创新课时精练系列答案

创新设计课堂讲义系列答案

创新优化新天地试卷系列答案

高中得分王系列答案

激活思维智能优选卷系列答案

金榜名卷复习冲刺卷系列答案

金东方文化五练一测系列答案

同步检测三级跳系列答案

课堂达优期末冲刺100分系列答案

相关题目

有一个长方体模型，它的长为2×103cm，宽为1.5×102cm，高为1.2×102cm，它的体积是多少立方厘米？

3.6×107(cm3) 【解析】试题分析：长方体的体积=长×宽×高，根据同底数幂的乘法计算法则得出答案．试题解析：V= 答：它的体积是立方厘米．

说明：从(A)，(B)两题中任选一题作答．

春节前夕，便民超市把一批进价为每件12元的商品，以每件定价20元销售，每天能售出240件．销售一段时间后发现：如果每件涨价1元，那么每天就少售出20件；如果每件降价1元，那么每天能多售出40件．

(A)在降价的情况下，要使该商品每天的销售盈利为1800元，每件应降价多少元？

(B)为了使该商品每天销售盈利为1980元，每件应定价为多少元？

我选择：__________.

（A）要使该商品每天的销售盈利为1800元，每件应降价3元．(B) 为了使商品每天销售盈利为1980元，每件应定价为21元或23元．【解析】试题分析：若选（A）设每件商品应降价x元，根据“（20-x-进价）（每天售出的数量+40x）=每天利润，”列出方程求解即可；若选（B）①设每件商品应降价x元，根据“（20-x-进价）（每天售出的数量+40x）=每天利润，”列出方程，此时方程无实数根；②...

在平面直角坐标系中，反比例函数y=的图象位于（）

A. 第二、四象限 B. 第一、三象限 C. 第一、四象限 D. 第三、四象限

B 【解析】试题分析：∵k=1>0，∴反比例函数的图象位于第一、三象限．故选B．

如图，在矩形ABCD中，AB=6cm，AD=8cm，点P从点B出发，沿对角线BD向点D匀速运动，速度为4cm/s，过点P作PQ⊥BD交BC于点Q，以PQ为一边作正方形PQMN，使得点N落在射线PD上．点O从点D出发，沿DC向点C匀速运动，速度为3cm/s，以O为圆心，1cm半径作⊙O．点P与点D同时出发，设它们的运动时间为t（单位：s）（0≤t≤）．

（1）如图1，连接DQ，若DQ平分∠BDC，则t的值为　　s；

（2）如图2，连接CM，设△CMQ的面积为S，求S关于t的函数关系式；

（3）在运动过程中，当t为何值时，⊙O与MN第一次相切？

（1）1s; （2）S=﹣t2+t；（3）. 【解析】试题分析：（1）由△DQC≌△DQP，推出DP=DC=6，在Rt△ADB中，BD=10，推出PB=4即可解决问题；（2）过点M作MH⊥BC于点H，证明△HMQ∽△PQB，，由=，得MH=t，即可求得△CMQ的面积；（3）设⊙O与MN相切于点E，连接OE，作OF⊥BD于点F，可证得△DFO∽△DCB，由此即可解得：t...

（2016湖北省武汉市）如图，在四边形ABCD中，∠ABC＝90°，AB＝3，BC＝4，CD＝10，DA＝，则BD的长为_______．

．【解析】作DM⊥BC，交BC延长线于M，连接AC，如图所示：则∠M=90°， ∴∠DCM+∠CDM=90°， ∵∠ABC=90°，AB=3，BC=4， ∴AC2=AB2+BC2=25， ∵CD=10，AD=5， ∴AC2+CD2=AD2， ∴△ACD是直角三角形，∠ACD=90°， ∴∠ACB+∠DCM=90°， ∴∠ACB=∠CD...

如图，在矩形ABCD中，E是AD边的中点，BE⊥AC，垂足为点F，分析下列四个结论：①△AEF∽△CAB；②CF=2AF；③S△ABF：S四边形CDEF=2：5；④cos∠CAD=．其中正确的结论有（　　）．

A. 4个 B. 3个 C. 2个 D. 1个

A 【解析】∵四边形ABCD是矩形， ∴AD∥BC，∠ABC=90°， ∴∠EAC=∠ACB， ∵BE⊥AC， ∴∠ABC=∠AFE=90°， ∴△AEF∽△CAB，故①正确； ∵AD∥BC， ∴△AEF∽△CBF， ∴， ∵AE=AD=BC， ∴， ∴CF=2AF，故②正确； ∵△AEF∽△CBF， ∴EF：BF...

（6a3b2+14a2c）÷a2等于_______；

6ab2+14c 【解析】（6a3b2+14a2c）÷a2=6a3b2÷a2+14a2c÷a2=6ab2+14c, 故答案为：6ab2+14c.

如图所示，按各组角的位置判断错误的是（）

A. ∠1和∠2是同旁内角 B. ∠3和∠4是内错角

C. ∠5和∠6是同旁内角 D. ∠5和∠7是同旁内角

C 【解析】根据同位角、内错角、同旁内角的定义进行解答即可．【解析】 ∠1和∠2是同旁内角，故A选项正确； ∠3和∠4是内错角，故B选项正确； ∠5和∠6不是同旁内角，故C选项错误； ∠5和∠7是同旁内角，故D选项正确；，故选：C.