已知不等式组$\left\{\begin{array}{l}{3x-4≤5x-2}\\{2x-3＜\frac{x+3}{2}}\end{array}\right.$.求此不等式组的整数解．题目和参考答案——青夏教育精英家教网—

题目内容

10．已知不等式组$\left\{\begin{array}{l}{3x-4≤5x-2}\\{2x-3＜\frac{x+3}{2}}\end{array}\right.$，求此不等式组的整数解．

分析首先分别求出两个不等式组的解集，再根据“大小小大中间找”可得不等式组的解集，再找出符合条件的整数即可．

解答解：$\left\{\begin{array}{l}{3x-4≤5x-2①}\\{2x-3＜\frac{x+3}{2}②}\end{array}\right.$，
由①得：x≥-1，
由②得：x＜3，
∴不等式组的解集是-1≤x＜3，
∴不等式组的整数解是-1，0，1，2．

点评此题主要考查了不等式组的解法及整数解的确定．求不等式组的解集，应遵循以下原则：同大取较大，同小取较小，大小小大中间找，大大小小解不了．

练习册系列答案

1．解方程：$\frac{1}{x-3}$-1=$\frac{2}{3-x}$．

a²+a³=a⁵

a²•a³=a⁶

（a²）³=a⁶

（$\frac{a}{2}$）²=$\frac{{a}^{2}}{2}$

5．已知：（a-b）²=9；（a+b）²=25，则a²+b²=（　　）

15．“x的3倍与y的和不小于2”用不等式可表示为（　　）

2．计算：
（1）$\sqrt{24}$×$\sqrt{\frac{1}{3}}$-4$\sqrt{\frac{1}{8}}$×（1-$\sqrt{2}$）⁰+$\sqrt{0.5}$
（2）（3$\sqrt{5}$+5$\sqrt{3}$）（-3$\sqrt{5}$+5$\sqrt{3}$）-（$\sqrt{48}$+$\frac{1}{4}$$\sqrt{3}$）÷$\sqrt{27}$．

19．

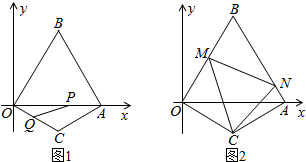已知：如图（1），△OAB是边长为2的等边三角形，0A在x轴上，点B在第一象限内；△OCA是一个等腰三角形，OC=AC，顶点C在第四象限，∠C=120°．现有两动点P、Q分别从A、O两点同时出发，点Q以每秒1个单位的速度沿OC向点C运动，点P以每秒3个单位的速度沿A→O→B运动，当其中一个点到达终点时，另一个点也随即停止．
（1）求在运动过程中形成的△OPQ的面积S与运动的时间t之间的函数关系，并写出自变量t的取值范围；
（2）在线段OA上（点O、A除外）存在点D，使得△OCD为等腰三角形，请直接写出所有符合条件的点D的坐标；
（3）如图（2），现有∠MCN=60°，其两边分别与OB、AB交于点M、N，连结MN．将∠MCN绕着C点旋转（0°＜旋转角＜60°），使得M、N始终在边OB和边AB上．试判断在这一过程中，△BMN的周长是否发生变化？若没有变化，请求出其周长；若发生变化，请说明理由．

20．九（1）班第5学习小组共有2位女生和3位男生．一次数学课上，老师随机让该学习小组的2位同学上台演示解题过程（每个同学上台演示的可能性相同），则上台演示解题过程的2位同学都是女生的概率等于（　　）

试题分类