题目内容
(1)解分式方程:
+
=1;
(2)解分式方程:
=2-
;
(3)先化简,再求值:(1-
)÷
,然后从-2≤x≤2的范围内选取一个合适的整数作为x的值代入求值.
| x |
| x-1 |
| 2 |
| x |
(2)解分式方程:
| 3 |
| x-3 |
| x |
| 3-x |
(3)先化简,再求值:(1-
| 1 |
| x-1 |
| x2-4x+4 |
| x2-1 |
考点:分式的化简求值,解分式方程
专题:
分析:(1)两边同时乘以x(x-1),转化为整式方程,解答即可;
(2)两边同时乘以x-3,转化为整式方程,解答即可;
(3)将括号内的部分通分相加,将除法转化为乘法,因式分解后约分即可.
(2)两边同时乘以x-3,转化为整式方程,解答即可;
(3)将括号内的部分通分相加,将除法转化为乘法,因式分解后约分即可.
解答:解:(1)两边同时乘以x(x-1),得x2+2(x-1)=x(x-1),
化简,得2x-2=-x,
解得x=
;
检验:当x=
时,x(x-1)≠0,故x=
是原分式方程的解.
(2)两边同时乘以x-3,得3=2(x-3)+x,
去括号,得3=2x-6+x,
解得,x=3;
检验:当x=3时,x-3=0,故原分式方程无解.
(3)原式=(
-
)•
=
•
=
;
当x=-2时,原式=
(或当x=0时,原式=-
).
化简,得2x-2=-x,
解得x=
| 2 |
| 3 |
检验:当x=
| 2 |
| 3 |
| 2 |
| 3 |
(2)两边同时乘以x-3,得3=2(x-3)+x,
去括号,得3=2x-6+x,
解得,x=3;
检验:当x=3时,x-3=0,故原分式方程无解.
(3)原式=(
| x-1 |
| x-1 |
| 1 |
| x-1 |
| (x-1)(x+1) |
| (x-2)2 |
=
| x-2 |
| x-1 |
| (x-1)(x+1) |
| (x-2)2 |
=
| x+1 |
| x-2 |
当x=-2时,原式=
| 1 |
| 4 |
| 1 |
| 2 |
点评:本题考查了分式方程和分式的化简求值,能找到最简公分母,熟悉因式分解是解答此类题目的关键.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
若a<-2,则下列函数:①y=-ax+1②y=ax③y=
(x>0)④y=(a+1)x,其中y随x的增大而增大的是( )
| a |
| x |
| A、①② | B、②③ | C、③④ | D、①③ |
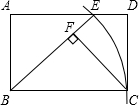 如图,在矩形ABCD中,AB=3,BC=5,以顶点B为圆心,边BC长为半径画弧,交AD边于点E,连结BE,过C点作CF⊥BE于F.
如图,在矩形ABCD中,AB=3,BC=5,以顶点B为圆心,边BC长为半径画弧,交AD边于点E,连结BE,过C点作CF⊥BE于F.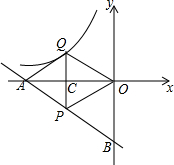 如图,一次函数y=-
如图,一次函数y=- 如图,AB∥CD,∠B=∠D=50°,
如图,AB∥CD,∠B=∠D=50°,