题目内容
2.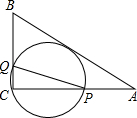 如图,在△ABC中,AB=10,AC=8,BC=6,经过点C且与边AB相切的动圆与CA,CB分别相交于点P,Q,则线段PQ的最小值( )
如图,在△ABC中,AB=10,AC=8,BC=6,经过点C且与边AB相切的动圆与CA,CB分别相交于点P,Q,则线段PQ的最小值( )| A. | 5 | B. | 4$\sqrt{2}$ | C. | 4.75 | D. | 4.8 |
分析 设QP的中点为F,圆F与AB的切点为D,连接FD,连接CF,CD,则有FD⊥AB;由勾股定理的逆定理知,△ABC是直角三角形,FC+FD=PQ,由三角形的三边关系知,FC+FD>CD;只有当点F在CD上时,FC+FD=PQ有最小值,最小值为CD的长,即当点F在直角三角形ABC的斜边AB的高CD上时,PQ=CD有最小值,由直角三角形的面积公式知,此时CD=BC•AC÷AB=4.8.
解答 解:线段PQ长度的最小值时,PQ为圆的直径,
如图,设QP的中点为F,圆F与AB的切点为D,连接FD、CF、CD,
∵圆F与AB相切,∴FD⊥AB,
∵AB=5,AC=4,BC=3,
∴∠ACB=90°,FC+FD=PQ,
∴CF+FD>CD,且PQ为圆F的直径,
∵当点F在直角三角形ABC的斜边AB的高上CD时,PQ=CD有最小值,即CD为圆F的直径,
且S△ABC=$\frac{1}{2}$BC•CA=$\frac{1}{2}$CD•AB,
∴CD=$\frac{BC•AC}{AB}$=4.8,即PQ的最小值为4.8,
故选:D.
点评 此题考查了切线的性质,垂线段最短,圆周角定理,以及直角三角形面积的求法,其中根据题意得:当点F在直角三角形ABC的斜边AB的高上CD时,PQ=CD为最小值是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.某小组5名同学在一周内参加家务劳动的时间如表所示,关于“劳动时间”的这组数据,以下说法正确的是( )
| 动时间(小时) | 3 | 3.5 | 4 | 4.5 |
| 人数 | 1 | 1 | 2 | 1 |
| A. | 中位数是4,平均数是3.75 | B. | 众数是4,平均数是3.75 | ||
| C. | 中位数是4,平均数是3.8 | D. | 众数是2,平均数是3.8 |
14.方程(x-2)(x-4)=0的两个根是等腰三角形的底和腰,则这个等腰三角形的周长为( )
| A. | 6 | B. | 8 | C. | 10 | D. | 8或10 |
11.下列运算正确的是( )
| A. | an•a2=a2n | B. | a3•a2=a6 | C. | an•(a2)n=a2n+2 | D. | a2n-3÷a-3=a2n |