题目内容
17.直线AB与⊙O相切于点B,C是⊙O与OA的交点,点D是⊙O上的动点(D与B、C不重合),若∠A=30°,求∠BDC的度数为30°或150°.分析 根据题意可以画出相应的图形,利用分类讨论的数学思想和切线的性质,同弧所对的圆周角和圆心角的关系可以求得∠BDC的度数.
解答  解:如右图所示,
解:如右图所示,
∵直线AB与⊙O相切于点B,C是⊙O与OA的交点,点D是⊙O上的动点(D与B、C不重合),
∴∠OBA=90°,
∵∠A=30°,
∴∠BOA=60°,
当点D在劣弧BC上时,∠BDC=180°-(60°÷2)=150°,
当点D在优弧BC上时,∠BDC=$\frac{1}{2}∠BOA=30°$,
故答案为:30°或150°.
点评 本题考查切线的性质,解答本题的关键是明确题意,找出所求问题需要的条件,利用分类讨论的数学思想解答.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.在△ABC中,PA=PB=PC,则点P是△ABC( )
| A. | 三条高的交点 | B. | 三条中线的交点 | ||
| C. | 三边垂直平分线交点 | D. | 三条角平分线的交点 |
2.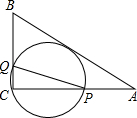 如图,在△ABC中,AB=10,AC=8,BC=6,经过点C且与边AB相切的动圆与CA,CB分别相交于点P,Q,则线段PQ的最小值( )
如图,在△ABC中,AB=10,AC=8,BC=6,经过点C且与边AB相切的动圆与CA,CB分别相交于点P,Q,则线段PQ的最小值( )
 如图,在△ABC中,AB=10,AC=8,BC=6,经过点C且与边AB相切的动圆与CA,CB分别相交于点P,Q,则线段PQ的最小值( )
如图,在△ABC中,AB=10,AC=8,BC=6,经过点C且与边AB相切的动圆与CA,CB分别相交于点P,Q,则线段PQ的最小值( )| A. | 5 | B. | 4$\sqrt{2}$ | C. | 4.75 | D. | 4.8 |
7. 某工厂加工一批零件,为了提高工人工作积极性,工厂规定每名工人每次薪金如下:生产的零件不超过a件,则每件3元,超过a件,超过部分每件b元,如图是一名工人一天获得薪金y(元)与其生产的件数x(件)之间的函数关系式,则下列结论错误的是( )
某工厂加工一批零件,为了提高工人工作积极性,工厂规定每名工人每次薪金如下:生产的零件不超过a件,则每件3元,超过a件,超过部分每件b元,如图是一名工人一天获得薪金y(元)与其生产的件数x(件)之间的函数关系式,则下列结论错误的是( )
 某工厂加工一批零件,为了提高工人工作积极性,工厂规定每名工人每次薪金如下:生产的零件不超过a件,则每件3元,超过a件,超过部分每件b元,如图是一名工人一天获得薪金y(元)与其生产的件数x(件)之间的函数关系式,则下列结论错误的是( )
某工厂加工一批零件,为了提高工人工作积极性,工厂规定每名工人每次薪金如下:生产的零件不超过a件,则每件3元,超过a件,超过部分每件b元,如图是一名工人一天获得薪金y(元)与其生产的件数x(件)之间的函数关系式,则下列结论错误的是( )| A. | a=20 | |
| B. | b=4 | |
| C. | 若工人甲一天获得薪金180元,则他共生产50件 | |
| D. | 若工人乙一天生产m(件),则他获得薪金4m元 |
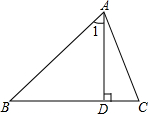 如图,AD是△ABC的高,∠1=∠B,∠C=65°,则∠BAC=70°.
如图,AD是△ABC的高,∠1=∠B,∠C=65°,则∠BAC=70°.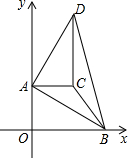 如图,在平面直角坐标系中,O为原点,点A(0,8),点B(m,0),且m>0.把△AOB绕点A逆时针旋转90°,得△ACD,点O,B旋转后的对应点为C,D.
如图,在平面直角坐标系中,O为原点,点A(0,8),点B(m,0),且m>0.把△AOB绕点A逆时针旋转90°,得△ACD,点O,B旋转后的对应点为C,D.