题目内容
15．
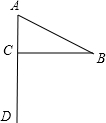如图，一面小红旗，其中∠A=60°，∠B=30°，则∠BCA=90°．求解的直接依据是（ ）| A． | 三角形内角和定理 | B． | 三角形外角和定理 | ||
| C． | 多边形内角和公式 | D． | 多边形外角和公式 |
分析 三角形已知两个角的度数，利用三角形内角和为180度可得第三个角的度数．
解答 解：∵∠A=60°，∠B=30°，
∴∠BCA=180°-60°-30°=90°（三角形内角和定理），
故选：A．
点评 此题主要考查了多边形的内角，关键是掌握三角形内角和为180度．
练习册系列答案
小学夺冠AB卷系列答案
相关题目
20．
把一张长方形纸条按图中，那样折叠后，若得到∠AOB′=70°，则∠B′OG的角度是（ ）
把一张长方形纸条按图中，那样折叠后，若得到∠AOB′=70°，则∠B′OG的角度是（ ）| A． | 55° | B． | 65° | C． | 45° | D． | 50° |
7．y=-（x+1）2+k上有A（-$\sqrt{2}$，y1），B（$\sqrt{2}$，y2）两点，则y1，y2的大小关系为（ ）
| A． | y1＞y2 | B． | y1＜y2 | C． | y1≥y2 | D． | y1≤y2 |
4．某广场地面铺满了边长为36cm的正六边形地砖，现在向上抛掷半径为6$\sqrt{3}$cm的圆碟，圆碟落地后与地砖间的间隙不相交的概率为（ ）
| A． | $\frac{4}{9}$ | B． | $\frac{5}{9}$ | C． | $\frac{2}{3}$ | D． | $\frac{\sqrt{3}}{3}$ |
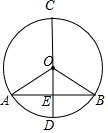如图所示，AB是⊙O的一条弦，OD⊥AB，垂足为E，交⊙O于点C、D，