题目内容
4.某广场地面铺满了边长为36cm的正六边形地砖,现在向上抛掷半径为6$\sqrt{3}$cm的圆碟,圆碟落地后与地砖间的间隙不相交的概率为( )| A. | $\frac{4}{9}$ | B. | $\frac{5}{9}$ | C. | $\frac{2}{3}$ | D. | $\frac{\sqrt{3}}{3}$ |
分析 欲使圆碟不压地砖间的间隙,则圆碟的圆心必须落在与地砖同中心、且边与地砖边彼此平行、距离为6$\sqrt{3}$cm的小正六边形内,从而计算这个小正多边形的面积,小正多边形与正六边形的面积之比即为所求.
解答 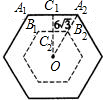 解:欲使圆碟不压地砖间的间隙,则圆碟的圆心必须落在与地砖同中心、且边与地砖边彼此平行、距离为6$\sqrt{3}$cm的小正六边形内(如图).作OC1⊥A1A2,且C1C2=6$\sqrt{3}$cm.
解:欲使圆碟不压地砖间的间隙,则圆碟的圆心必须落在与地砖同中心、且边与地砖边彼此平行、距离为6$\sqrt{3}$cm的小正六边形内(如图).作OC1⊥A1A2,且C1C2=6$\sqrt{3}$cm.
因A1A2=A2O=36,A2C1=18,所以,
C1O=$\frac{\sqrt{3}}{2}$A2O=18$\sqrt{3}$.
则C2O=C1O-C1C2=12$\sqrt{3}$.
又因为C2O=$\sqrt{3}$B2O,所以,
B2O=$\frac{2}{\sqrt{3}}$C2O=$\frac{2}{\sqrt{3}}$×12$\sqrt{3}$=24.
而B1B2=B2O,则小正六边形的边长为24cm.
故所求概率为
P=$\frac{小正六边形的面积}{正六边形地砖面积}$=($\frac{{B}_{1}{B}_{2}}{{A}_{1}{A}_{2}}$)2=($\frac{24}{36}$)2=$\frac{4}{9}$.
故选A.
点评 本题考查的是几何概率、正多边形和圆的综合利用,关键是理清题意,找准之间的关系进行解题.

练习册系列答案
 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
15.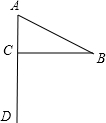 如图,一面小红旗,其中∠A=60°,∠B=30°,则∠BCA=90°.求解的直接依据是( )
如图,一面小红旗,其中∠A=60°,∠B=30°,则∠BCA=90°.求解的直接依据是( )
 如图,一面小红旗,其中∠A=60°,∠B=30°,则∠BCA=90°.求解的直接依据是( )
如图,一面小红旗,其中∠A=60°,∠B=30°,则∠BCA=90°.求解的直接依据是( )| A. | 三角形内角和定理 | B. | 三角形外角和定理 | ||
| C. | 多边形内角和公式 | D. | 多边形外角和公式 |
19.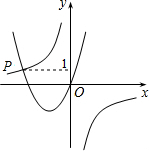 如图,已知函数y=-$\frac{3}{x}$与y=ax2+bx(a>0,b>0)的图象交于点P,点P的纵坐标为1,则关于x的方程ax2+bx+$\frac{3}{x}$=0的解为( )
如图,已知函数y=-$\frac{3}{x}$与y=ax2+bx(a>0,b>0)的图象交于点P,点P的纵坐标为1,则关于x的方程ax2+bx+$\frac{3}{x}$=0的解为( )
 如图,已知函数y=-$\frac{3}{x}$与y=ax2+bx(a>0,b>0)的图象交于点P,点P的纵坐标为1,则关于x的方程ax2+bx+$\frac{3}{x}$=0的解为( )
如图,已知函数y=-$\frac{3}{x}$与y=ax2+bx(a>0,b>0)的图象交于点P,点P的纵坐标为1,则关于x的方程ax2+bx+$\frac{3}{x}$=0的解为( )| A. | x=3 | B. | x=1 | C. | x=-3 | D. | 无解 |
13. 如图,AD是△ABC的外角∠EAC的平分线,与△ABC的外接圆交于点D,则图中与∠EAD相等的角(不包括∠EAD)有( )
如图,AD是△ABC的外角∠EAC的平分线,与△ABC的外接圆交于点D,则图中与∠EAD相等的角(不包括∠EAD)有( )
 如图,AD是△ABC的外角∠EAC的平分线,与△ABC的外接圆交于点D,则图中与∠EAD相等的角(不包括∠EAD)有( )
如图,AD是△ABC的外角∠EAC的平分线,与△ABC的外接圆交于点D,则图中与∠EAD相等的角(不包括∠EAD)有( )| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
14.在△ABC中,∠A,∠B,∠C的对边分别是a,b,c,则下列条件不能判定△ABC是直角三角形的是( )
| A. | ∠A=∠B-∠C | B. | ∠A:∠B:∠C=1:3:4 | C. | $a:b:c=1:\sqrt{2}:3$ | D. | a2+c2=b2 |