题目内容
5.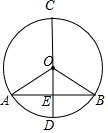 如图所示,AB是⊙O的一条弦,OD⊥AB,垂足为E,交⊙O于点C、D,
如图所示,AB是⊙O的一条弦,OD⊥AB,垂足为E,交⊙O于点C、D,(1)若∠AOD=52°,求∠DOB的度数;
(2)若AE=$\sqrt{7}$,ED=1,求CD的长.
分析 (1)根据垂径定理得到弧AD=弧BD,然后根据相等的弧所对的圆心角相等求解;
(2)在直角△AOE中利用勾股定理即可列方程求得半径,则CD即可求得.
解答 解:(1)∵OD⊥AB,
∴$\widehat{AD}$=$\widehat{BD}$,
∴∠DOB=∠AOD=52°;
(2)设半径是r,
在直角△AOE中,OE2+AE2=0A2,
则(r-1)2+($\sqrt{7}$)2=r2,
解得r=4,
则CD=2r=8.
点评 本题考查了垂径定理,在圆中半径、弦长和弦心距的计算一般就是转化为直角三角形的计算.

练习册系列答案
相关题目
15.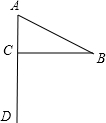 如图,一面小红旗,其中∠A=60°,∠B=30°,则∠BCA=90°.求解的直接依据是( )
如图,一面小红旗,其中∠A=60°,∠B=30°,则∠BCA=90°.求解的直接依据是( )
 如图,一面小红旗,其中∠A=60°,∠B=30°,则∠BCA=90°.求解的直接依据是( )
如图,一面小红旗,其中∠A=60°,∠B=30°,则∠BCA=90°.求解的直接依据是( )| A. | 三角形内角和定理 | B. | 三角形外角和定理 | ||
| C. | 多边形内角和公式 | D. | 多边形外角和公式 |
13. 如图,AD是△ABC的外角∠EAC的平分线,与△ABC的外接圆交于点D,则图中与∠EAD相等的角(不包括∠EAD)有( )
如图,AD是△ABC的外角∠EAC的平分线,与△ABC的外接圆交于点D,则图中与∠EAD相等的角(不包括∠EAD)有( )
 如图,AD是△ABC的外角∠EAC的平分线,与△ABC的外接圆交于点D,则图中与∠EAD相等的角(不包括∠EAD)有( )
如图,AD是△ABC的外角∠EAC的平分线,与△ABC的外接圆交于点D,则图中与∠EAD相等的角(不包括∠EAD)有( )| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
14.在△ABC中,∠A,∠B,∠C的对边分别是a,b,c,则下列条件不能判定△ABC是直角三角形的是( )
| A. | ∠A=∠B-∠C | B. | ∠A:∠B:∠C=1:3:4 | C. | $a:b:c=1:\sqrt{2}:3$ | D. | a2+c2=b2 |

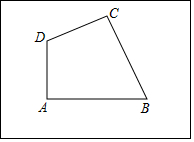 小亮家的房前有一块矩形的空地,空地上有四棵银杏树A、B、C,D,且∠A=∠C=90°,小亮想建一个圆形花坛,使四棵树都在花坛的边上.小亮请小明帮他设计方案:
小亮家的房前有一块矩形的空地,空地上有四棵银杏树A、B、C,D,且∠A=∠C=90°,小亮想建一个圆形花坛,使四棵树都在花坛的边上.小亮请小明帮他设计方案: