题目内容
7.y=-(x+1)2+k上有A(-$\sqrt{2}$,y1),B($\sqrt{2}$,y2)两点,则y1,y2的大小关系为( )| A. | y1>y2 | B. | y1<y2 | C. | y1≥y2 | D. | y1≤y2 |
分析 把A、B两点的坐标分别代入解析式,可用k分别表示出y1,y2,则可比较其大小.
解答 解:
∵A(-$\sqrt{2}$,y1),B($\sqrt{2}$,y2)在抛物线上,
∴y1=-(-$\sqrt{2}$+1)2+k=2$\sqrt{2}$-3+k,y2=-($\sqrt{2}$+1)2+k=-2$\sqrt{2}$-3+k,
∵2$\sqrt{2}$-3>-2$\sqrt{2}$-3,
∴2$\sqrt{2}$-3+k>-2$\sqrt{2}$-3+k,即y1>y2,
故选A.
点评 本题主要考查二次函数图象上点的坐标特征,掌握函数图象上的点的坐标满足函数解析式是解题的关键.

练习册系列答案
相关题目
4.如果多项式x2-5x+m分解因式的结果为(x-3)(x+n),那么m,n的值分别为( )
| A. | m=-2,n=6 | B. | m=2,n=-6 | C. | m=6,n=-2 | D. | m=-6,n=-2 |
18.一个数除以9的商为x,余数为2,则这个数为( )
| A. | 9x+2 | B. | 9x-2 | C. | -$\frac{2}{9}$x | D. | $\frac{2}{9}$x |
15.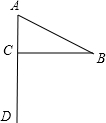 如图,一面小红旗,其中∠A=60°,∠B=30°,则∠BCA=90°.求解的直接依据是( )
如图,一面小红旗,其中∠A=60°,∠B=30°,则∠BCA=90°.求解的直接依据是( )
 如图,一面小红旗,其中∠A=60°,∠B=30°,则∠BCA=90°.求解的直接依据是( )
如图,一面小红旗,其中∠A=60°,∠B=30°,则∠BCA=90°.求解的直接依据是( )| A. | 三角形内角和定理 | B. | 三角形外角和定理 | ||
| C. | 多边形内角和公式 | D. | 多边形外角和公式 |
2.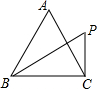 如图,在边长为3的等边△ABC中,过点C作垂直于BC的直线交∠ABC的平分线于点P,则点P到边AB所在直线的距离为( )
如图,在边长为3的等边△ABC中,过点C作垂直于BC的直线交∠ABC的平分线于点P,则点P到边AB所在直线的距离为( )
 如图,在边长为3的等边△ABC中,过点C作垂直于BC的直线交∠ABC的平分线于点P,则点P到边AB所在直线的距离为( )
如图,在边长为3的等边△ABC中,过点C作垂直于BC的直线交∠ABC的平分线于点P,则点P到边AB所在直线的距离为( )| A. | $\frac{\sqrt{3}}{4}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\sqrt{3}$ |
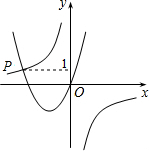 如图,已知函数y=-$\frac{3}{x}$与y=ax2+bx(a>0,b>0)的图象交于点P,点P的纵坐标为1,则关于x的方程ax2+bx+$\frac{3}{x}$=0的解为( )
如图,已知函数y=-$\frac{3}{x}$与y=ax2+bx(a>0,b>0)的图象交于点P,点P的纵坐标为1,则关于x的方程ax2+bx+$\frac{3}{x}$=0的解为( )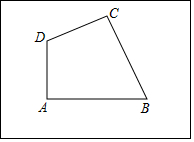 小亮家的房前有一块矩形的空地,空地上有四棵银杏树A、B、C,D,且∠A=∠C=90°,小亮想建一个圆形花坛,使四棵树都在花坛的边上.小亮请小明帮他设计方案:
小亮家的房前有一块矩形的空地,空地上有四棵银杏树A、B、C,D,且∠A=∠C=90°,小亮想建一个圆形花坛,使四棵树都在花坛的边上.小亮请小明帮他设计方案: