题目内容
6.(1)x2-4x-6=0(2)3x(x+2)-5(x+2)=0.
分析 (1)利用配方法解方程;
(2)提公因式x+2,则(x+2)(3x-5)=0,利用分解因式法解方程.
解答 解:(1)x2-4x-6=0,
x2-4x+4=6+4,
(x-2)2=10,
x=2±$\sqrt{10}$,
x1=2-$\sqrt{10}$,x2=2-$\sqrt{10}$;
(2)3x(x+2)-5(x+2)=0,
(x+2)(3x-5)=0,
x+2=0或3x-5=0,
x1=-2,x2=$\frac{5}{3}$.
点评 本题是解一元二次方程,解一元二次方程时首先考虑能否运用因式分解法解方程,如第2个方程,可以利用提公因式法解方程;如果不能,若一次项系数是偶数时,且二次项系数为1时,可以考虑运用配方法解方程,如第1个方程,利用配方法解方程.

练习册系列答案
相关题目
4.如果多项式x2-5x+m分解因式的结果为(x-3)(x+n),那么m,n的值分别为( )
| A. | m=-2,n=6 | B. | m=2,n=-6 | C. | m=6,n=-2 | D. | m=-6,n=-2 |
18.一个数除以9的商为x,余数为2,则这个数为( )
| A. | 9x+2 | B. | 9x-2 | C. | -$\frac{2}{9}$x | D. | $\frac{2}{9}$x |
15.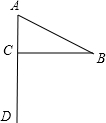 如图,一面小红旗,其中∠A=60°,∠B=30°,则∠BCA=90°.求解的直接依据是( )
如图,一面小红旗,其中∠A=60°,∠B=30°,则∠BCA=90°.求解的直接依据是( )
 如图,一面小红旗,其中∠A=60°,∠B=30°,则∠BCA=90°.求解的直接依据是( )
如图,一面小红旗,其中∠A=60°,∠B=30°,则∠BCA=90°.求解的直接依据是( )| A. | 三角形内角和定理 | B. | 三角形外角和定理 | ||
| C. | 多边形内角和公式 | D. | 多边形外角和公式 |
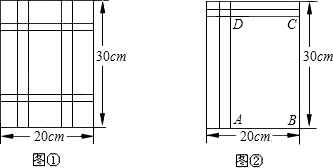
 小明想把一长为25cm,宽为20cm的长方形硬纸片做成一个无盖的长方体盒子,于是在长方形纸片的四个角各剪去一个相同的小正方形.
小明想把一长为25cm,宽为20cm的长方形硬纸片做成一个无盖的长方体盒子,于是在长方形纸片的四个角各剪去一个相同的小正方形.