题目内容
如图,长方形OABC中,O为平面直角坐标系的原点,A、C两点的坐标分别为(3,0),(0,5),点B在第一象限内.

(1)如图1,写出点B的坐标( );
(2)如图2,若过点C的直线CD交AB于点D,且把长方形OABC的周长分为3:1两部分,则点D的坐标( );
(3)如图3,将(2)中的线段CD向下平移,得到C′D′,使C′D′平分长方形OABC的面积,则此时点D′的坐标是( ).

(1)如图1,写出点B的坐标(
(2)如图2,若过点C的直线CD交AB于点D,且把长方形OABC的周长分为3:1两部分,则点D的坐标(
(3)如图3,将(2)中的线段CD向下平移,得到C′D′,使C′D′平分长方形OABC的面积,则此时点D′的坐标是(
考点:坐标与图形性质,三角形的面积,坐标与图形变化-平移
专题:
分析:(1)根据矩形的对边相等可得BC=OA,AB=OC,然后写出点B的坐标即可;
(2)先求出长方形OABC的周长,然后求出被分成两个部分的长度,判断出点D一定在AB上,再求出BD的长度即可得解;
(3)先用待定系数法求出直线CD的解析式,根据线段CD向下平移,得到C′D′,设处直线C′D′的解析式,再求出矩形OABC的中心坐标,代入直线C′D′的解析式即可得出结论.
(2)先求出长方形OABC的周长,然后求出被分成两个部分的长度,判断出点D一定在AB上,再求出BD的长度即可得解;
(3)先用待定系数法求出直线CD的解析式,根据线段CD向下平移,得到C′D′,设处直线C′D′的解析式,再求出矩形OABC的中心坐标,代入直线C′D′的解析式即可得出结论.
解答:解:(1)∵A(3,0),C(0,5),
∴OA=3,OC=5,
∵四边形OABC是长方形,
∴BC=OA=3,AB=OC=5,
∴点B的坐标为(3,5).
故答案为(3,5);
(2)长方形OABC的周长为:2(3+5)=16,
∵CD把长方形OABC的周长分为3:1两部分,
∴被分成的两部分的长分别为16×
=12,16×
=4,
①C→B→D长为4,点D一定在AB上,
∴BD=4-3=1,AD=5-BD=5-1=4,
∴点D的坐标为(3,4),
②C→B→A→O→D长为12时,点D在OC上,OD=1,不符合题意,
所以,点D的坐标为(3,4).
故答案为(3,4);
(3)设直线CD的解析式为y=kx+b(k≠0),
∵C(0,5),D(3,4),
∴
,解得
,
∴直线CD的解析式为y=-
x+5,
∵直线C′D′由直线CD平移而成,
∴设直线C′D′的解析式为y=-
x+5-a,
∵A(3,0),C(0,5),
∴矩形OABC的中心坐标为(
,
),
∵C′D′平分长方形OABC的面积,
∴直线C′D′过矩形OABC的中心,
∴
=-
×
+5-a,解得a=2,
∴D′(3,2).
故答案为:(3,2).
∴OA=3,OC=5,
∵四边形OABC是长方形,
∴BC=OA=3,AB=OC=5,
∴点B的坐标为(3,5).
故答案为(3,5);
(2)长方形OABC的周长为:2(3+5)=16,
∵CD把长方形OABC的周长分为3:1两部分,
∴被分成的两部分的长分别为16×
| 3 |
| 1+3 |
| 1 |
| 1+3 |
①C→B→D长为4,点D一定在AB上,
∴BD=4-3=1,AD=5-BD=5-1=4,
∴点D的坐标为(3,4),
②C→B→A→O→D长为12时,点D在OC上,OD=1,不符合题意,
所以,点D的坐标为(3,4).
故答案为(3,4);
(3)设直线CD的解析式为y=kx+b(k≠0),
∵C(0,5),D(3,4),
∴
|
|
∴直线CD的解析式为y=-
| 1 |
| 3 |
∵直线C′D′由直线CD平移而成,
∴设直线C′D′的解析式为y=-
| 1 |
| 3 |
∵A(3,0),C(0,5),
∴矩形OABC的中心坐标为(
| 3 |
| 2 |
| 5 |
| 2 |
∵C′D′平分长方形OABC的面积,
∴直线C′D′过矩形OABC的中心,
∴
| 5 |
| 2 |
| 1 |
| 3 |
| 3 |
| 2 |
∴D′(3,2).
故答案为:(3,2).
点评:本题考查的是坐标与图形性质,熟知矩形的性质与一次函数的性质是解答此题的关键.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
 已知A,B两点的坐标分别为(2,4),(7,2),
已知A,B两点的坐标分别为(2,4),(7,2), 如图所示,在直角梯形OABC中,CB∥OA,CB=8,OC=8,OA=16
如图所示,在直角梯形OABC中,CB∥OA,CB=8,OC=8,OA=16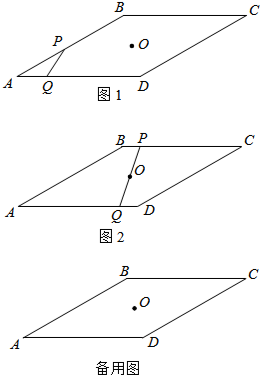 如图1,菱形ABCD中,∠A=30°,边长AB=10cm,在对称中心O处有一钉子.动点P,Q同时从点A出发,点P沿A→B→C方向以每秒2cm的速度运动,到点C停止,点Q沿2方向以每秒1cm的速度运动,到点D停止.P,Q两点用一条可伸缩的细橡皮筋连接,设t秒后橡皮筋扫过的面积为ycm2.
如图1,菱形ABCD中,∠A=30°,边长AB=10cm,在对称中心O处有一钉子.动点P,Q同时从点A出发,点P沿A→B→C方向以每秒2cm的速度运动,到点C停止,点Q沿2方向以每秒1cm的速度运动,到点D停止.P,Q两点用一条可伸缩的细橡皮筋连接,设t秒后橡皮筋扫过的面积为ycm2. 已知:如图,五边形ABCDE中,AE∥BC,∠A+∠B=α,∠C+∠D+∠E=β,猜想α与β的数量关系并写出你的证明.
已知:如图,五边形ABCDE中,AE∥BC,∠A+∠B=α,∠C+∠D+∠E=β,猜想α与β的数量关系并写出你的证明. 如图,长为50cm,宽为xcm的大长方形被分割为8小块,除阴影A、B外,其余6块是形状、大小完全相同的小长方形,其较短一边长为acm.
如图,长为50cm,宽为xcm的大长方形被分割为8小块,除阴影A、B外,其余6块是形状、大小完全相同的小长方形,其较短一边长为acm.