题目内容
 如图,P是正方形ABCD内一点,将△ABP绕点B按顺时针旋转90°到△CBP′,若PB=2
如图,P是正方形ABCD内一点,将△ABP绕点B按顺时针旋转90°到△CBP′,若PB=2| 2 |
考点:旋转的性质,等腰直角三角形,正方形的性质
专题:
分析:将△ABP绕点B按顺时针旋转90°到△CBP′,可得△PBP′是等腰直角三角形,继而可求得答案.
解答:解:∵将△ABP绕点B按顺时针旋转90°到△CBP′,
∴P′B=PB=2
,∠PBP′=90°,
∴PP′=
PB=4.
故答案为:4.
∴P′B=PB=2
| 2 |
∴PP′=
| 2 |
故答案为:4.
点评:此题考查了旋转的性质以及等腰直角三角形性质.此题难度不大,注意掌握旋转前后图形的对应关系,注意数形结合思想的应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
不等式x-2<0的解集在数轴上表示出来正确的是( )
A、 |
B、 |
C、 |
D、 |
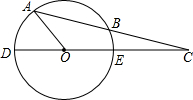 如图,DE为⊙O的直径,AB为⊙O的弦,延长AB与直线DE交于C,且BC等于圆的半径,已知∠AOD=54°,则∠ACD=( )
如图,DE为⊙O的直径,AB为⊙O的弦,延长AB与直线DE交于C,且BC等于圆的半径,已知∠AOD=54°,则∠ACD=( )| A、18° | B、22.5° |
| C、30° | D、15° |
若直角三角形的两条直角边各扩大一倍,则斜边( )
| A、不变 | B、扩大一倍 |
| C、扩大两倍 | D、扩大四倍 |
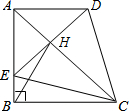 如图,在直角梯形ABCD中,AD∥BC,∠ABC=90°,AB=BC,E为AB边上一点,∠BCE=15°,且AE=AD.连接DE交对角线AC于H,连接BH.下列结论:
如图,在直角梯形ABCD中,AD∥BC,∠ABC=90°,AB=BC,E为AB边上一点,∠BCE=15°,且AE=AD.连接DE交对角线AC于H,连接BH.下列结论: 如图,抛物线y=ax2+bx+c顶点P坐标为(2,-1),与y轴交点坐标(0,3),将该抛物线沿图中P→Q方向平移
如图,抛物线y=ax2+bx+c顶点P坐标为(2,-1),与y轴交点坐标(0,3),将该抛物线沿图中P→Q方向平移 如图,在平面直角坐标系中,半圆O与x轴、y轴相交于A⊙O,B(0,-1),当一次函数y=-x+b与半圆O恰好只有一个公共点时,则常数b满足的条件为
如图,在平面直角坐标系中,半圆O与x轴、y轴相交于A⊙O,B(0,-1),当一次函数y=-x+b与半圆O恰好只有一个公共点时,则常数b满足的条件为