题目内容
 如图,在平面直角坐标系中,半圆O与x轴、y轴相交于A⊙O,B(0,-1),当一次函数y=-x+b与半圆O恰好只有一个公共点时,则常数b满足的条件为
如图,在平面直角坐标系中,半圆O与x轴、y轴相交于A⊙O,B(0,-1),当一次函数y=-x+b与半圆O恰好只有一个公共点时,则常数b满足的条件为考点:一次函数综合题
专题:
分析:b的值就是直线与y轴的交点的纵坐标,切直线当直线经过B时,一定同时经过点(1,0),再求出直线与圆在第四象限部分相切时b的值,即可写出b的取值范围.
解答: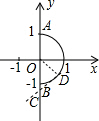 解:当一次函数y=-x+b,过点A时,b=1;
解:当一次函数y=-x+b,过点A时,b=1;
当直线经过B时,一定同时经过点(1,0),此时b=-1;
当直线与圆在第四象限部分相切时,设与y轴的交点是C,切点是D,则△OCD是等腰直角三角形,则OC=
=
,
故C的坐标是(-
,0).
故一次函数y=-x+b与半圆O恰好只有一个公共点时,常数b满足的条件为:-1<b≤1或b=-
.
故答案是:-1<b≤1或b=-
.
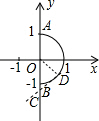 解:当一次函数y=-x+b,过点A时,b=1;
解:当一次函数y=-x+b,过点A时,b=1;当直线经过B时,一定同时经过点(1,0),此时b=-1;
当直线与圆在第四象限部分相切时,设与y轴的交点是C,切点是D,则△OCD是等腰直角三角形,则OC=
| 12+12 |
| 2 |
故C的坐标是(-
| 2 |
故一次函数y=-x+b与半圆O恰好只有一个公共点时,常数b满足的条件为:-1<b≤1或b=-
| 2 |
故答案是:-1<b≤1或b=-
| 2 |
点评:本题考查了一次函数的性质,以及直线与圆的位置关系,勾股定理,正确结合图形求出b的几个关键位置是关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
若不等式组
无解,则a的取值范围是( )
|
| A、a>-1 | B、a≥-1 |
| C、a≤1 | D、a<-1 |

 如图,P是正方形ABCD内一点,将△ABP绕点B按顺时针旋转90°到△CBP′,若PB=
如图,P是正方形ABCD内一点,将△ABP绕点B按顺时针旋转90°到△CBP′,若PB= 在平面直角坐标系中,△ABC的顶点坐标是A(O,3),B(-3,O),C(-2,O).点P为△ABC内一点,翻折△ABC得到△A1B1C1(点A、B、C的对应点分别为A1、B1、C1),使点P(m,n)翻折到P′(-m,n)处.
在平面直角坐标系中,△ABC的顶点坐标是A(O,3),B(-3,O),C(-2,O).点P为△ABC内一点,翻折△ABC得到△A1B1C1(点A、B、C的对应点分别为A1、B1、C1),使点P(m,n)翻折到P′(-m,n)处.